Proyecto de Soporte para Decisiones de Mantenimiento en Orica

Posted on mayo 6, 2011 by Ron Jenkins

Abstract

¿Entrega el monitoreo de condiciones el resultado que usted espera? ¿Podemos “ajustar las herramientas” y tomar una decisión de confiabilidad más fundamentada? El proyecto investigó  una herramienta de Soporte a la Decisión de Mantenimiento y como esta debería  ser utilizada  para mejorar las decisiones de confiabilidad basadas en la predicción de fallas. Se ha comprobado que la recolección y manipulación de los datos ha sido el reto más grande. Se demostró que para que el análisis de confiabilidad sea exitoso es de vital importancia la precisión con la que las fallas se registran en el CMMS (Computerized Maintenance Management System) e identificar cuáles modos de falla realmente ocurrieron y si efectivamente fallaron o fueron suspendidos. El esfuerzo necesario por el Ingeniero de Confiabilidad en realizar análisis de confiabilidad no tiene comparación con el requerido para la limpieza de los datos y su transformación en alguna forma analizable. Una vez que se eliminan las inconsistencias del estilo de la orden de trabajo, usando los métodos LRCM, se puede fácilmente utilizar el software de RA para llevar acabo análisis de confiabilidad.

I INTRODUCCIÓN

El presente documento ofrece una percepción acerca de los retos que enfrenta el Ingeniero de Confiabilidad antes de que él pueda explotar el software de Soporte de Decisiones de Mantenimiento. El propósito del presente estudio es aplicar esta herramienta [1] a bombas críticas en la Planta Laverton North Chloralkali de Orica en Australia. Allí ya existía el Monitoreo de Condiciones (CM). Sin embargo, se han presentado fallas inesperadas a raíz de lo cual, la necesidad de validar y mejorar el proceso CM adquirió la mayor importancia. Las decisiones basadas en confiabilidad pueden ser asistidas con tipos específicos de información relacionada con la operación y el mantenimiento de equipos. Sin embargo, es importante reconocer que grandes volúmenes de información CM no son garantía de buenos modelos de decisiones de mantenimiento basadas en condiciones, a menos que esa información refleje el deterioro de los modos de falla que realmente ocurren. Como sabemos cuáles variables de monitoreo de condiciones son importantes? Este proyecto intentará utilizar una herramienta de software que analiza la información de fallas de CMMS en conjunción con la información de monitoreo de condiciones con el fin de identificar aquellas variables monitoreadas que influyen en la probabilidad de que ocurran los modos de falla determinados cono objetivo. La metodología se aplica al Modelo de Riesgo Proporcional (PHM) [2] para determinar no solamente cuales variables monitoreadas son significativas, sino también la relación probabilística precisa entre esas variables y la falla de equipos. El principal objetivo de este estudio es entender la naturaleza de la información requerida para esto. El documento comentará una filosofía de adquisición, limpieza y transformación de información para programas de monitoreo de condiciones que den soporte a la toma de decisiones prácticas en mantenimiento.

II ALCANCE

El estudio fue imitado a cuatro conjuntos de bombas durante dos años, una muestra ciertamente pequeña. Estas bombas son todas bombas magnéticas con motores de inducción en servicio caustico, según se detalla en la Tabla 1 a continuación.

Etiqueta Descripción de la Bomba Modelo de la Bomba
P12111A Bomba Catholyte A Mando Magnético Tamaño 80
P12111B Bomba Catholyte A Mando Magnético Tamaño 80
P13005 Bomba Alimentación Evaporador Cáustica Magnetic Drive Size 40
P13006 Bomba Intermedia Cáustica Mando Magnético Tamaño 40
P12111AM Motor Bomba Catholyte A Motor de Inducción de  11kW
P12111BM Motor Bomba Catholyte B Motor de Inducción de  11kW
P13005M Motor Bomba Alimentación Evaporador Cáustica Motor de Inducción de  15kW
P13006M Motor Bomba Intermedia Cáustica Motor de Inducción de  15kW

III MODELOS DE PREDICCIÓN DE CONFIABILIDAD

Existen en el mercado muchas herramientas de software de predicción de confiabilidad. Una búsqueda básica en la web revela un buen número de vendedores, como por ejemplo [1], [2], [3]. El objetivo de este proyecto es probar uno de estos programas, EXAKT© en razón a que es uno de los pocos que enfrenta el reto de lograr decisiones verificables diariamente, basadas en las dos principales fuentes de información de mantenimiento disponibles: la(s) base(s) de datos CBM y la base de datos CMMS.

La predicción de confiabilidad no es nueva. Uno de los modelos mas ampliamente reconocidos fue desarrollado por Weibull en 1951 [4]. El desarrolló un método de análisis de fallas que proporcionaba predicciones de confiabilidad así como el nivel de confianza con el cual se podían aplicar dichas predicciones.

Distribución Weibull – tres de sus formas

Distribución acumulativa F(t)=1-e^{-\left(\frac{t}{n} \right)^{\beta}}

Riesgo h(t)=\frac{\beta}{\eta}\left( \frac{t}{\eta}\right)^{\beta -1}

Densidad de probabilidad f(t)=\frac{\beta}{\eta}\left(\frac{t}{\eta} \right)^{\beta-1}e^{\left(-\frac{t}{\eta} \right)^{\beta}}

Donde:
β (beta) es el parámetro de “forma”,
η (eta) es el parámetro de “escala”, y
t es la edad de trabajo del ítem o del modo de falla que se esté modelando.

Weibull también demostró que el parámetro de forma ß en su ecuación (arriba) que relaciona la confiabilidad con la edad proporciona una indicación del probable comportamiento de falla. Para un parámetro de forma de ß <1, el modelo de Weibull predice una mortalidad muy temprana debido a la deficiente calidad de materiales, instalación incorrecta, o procedimientos de arranque defectuosos. Si  ß =1 el comportamiento de falla es aleatorio, lo que significa que la rata de falla (o la probabilidad condicional de falla) es constante y no cambia con la edad o utilización.  Finalmente, para ß >1, el modelo Weibull predice que la rata de falla se incrementará con la edad debido a desgaste. Basados en que el modelo Weibull ha determinado que   ß =< 1 podemos concluir que los programas de reemplazo basados en edad, en lugar de mejorar el desempeño, podría, al contrario, llevar a costos innecesarios, tiempos de parada y una deficiente confiabilidad.  En caso que una estrategia de mantenimiento indique que un componente con falla aleatoria (con  ß = 1) debe ser reemplazado de manera preventiva en un intervalo igual a su MTBF = η, en ese caso, el 63% de las veces ese componente fallará antes del MP.

Para desarrollar un modelo Weibull solamente necesitamos determinar (estimando a partir de información histórica) valores para los parámetros ß y η. El modelo producirá una diversidad de puntos de información que revelen la relación entre edad y confiabilidad. Estas relaciones, al ser representadas de manera gráfica nos ayudan a comprender el comportamiento de falla basado en edad de los ítems y, más útil aun, sus modos de falla.

El problema de análisis basado en edad

Con análisis básico Weibull (basado en edad) la toma de decisiones prácticas se tornará problemática frecuentemente si las poblaciones estadísticas se mezclan, o si condiciones variantes influyen sobre unidades individuales de la muestra. En esos casos, el análisis Weibull básico tenderá a subestimar el parámetro de forma ß, lo que conducirá a subestimar la vida del equipo. La Figura 1 y la Figura 2 ilustran un problema general cuando los ingenieros de mantenimiento utilizan el análisis basado en edad para la toma de decisiones proactivas. El análisis puede frecuentemente conducir a frecuencias de reemplazo preventivo y costos más altos de lo necesario.

Figure 1 Weibull analysis of individual and combined data sets.
Figura 1 Análisis Weibull de conjuntos de datos individuales y combinados.
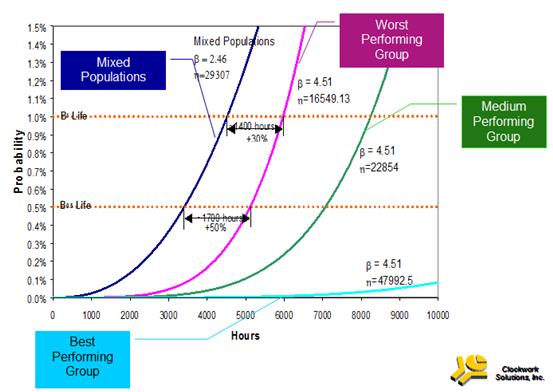
Figura 2 Gráficos de probabilidad temprana de vida de poblaciones estadísticas individuales y mezcladas – 3 conjuntos de datos cada uno produciendo un factor de forma Weibull de 4.51. El análisis Weibull de la población estadística mezclada, sin embargo, produce un factor de forma inferior de 2.46, con un significativo impacto en la vida pronosticada. (Ref. 7).

Además del problema de las poblaciones estadísticas mezcladas, el tomar decisiones individuales de reparar – ahora o continuar – operando, armados solamente con la edad del ítem, es de poco valor en las operaciones cotidianas. La edad, en el gráfico edad – confiabilidad es en esencia una mezcla que promedia los efectos de otras variables influyentes pero no – especificadas. La edad por si sola, por lo tanto, oculta la influencia de las condiciones individuales de operación de una unidad y de su condición actual, reflejada por su información de monitoreo de condición. Esta realidad ha conducido hacia un enfoque estratégico de mantenimiento llamado Mantenimiento Basado en Condiciones (CBM).

De qué manera se puede ampliar el análisis Weibull para cubrir CBM?

El Modelaje de Riesgos Proporcionales (PHM) amplia el método Weibull para cubrir la realidad actual CBM. Resuelve el problema de poblaciones estadísticas mezcladas al incluir, no solamente la edad, sino también otros significativos factores diferenciadores (operacionales y monitoreados) en el análisis. El procedimiento hace uso de los económicos computadores personales de hoy para manejar los intensivos requerimientos de computación.

PHM pretende “afilar la sierra” utilizando todos los factores significativos de predicción disponibles. Estos incluyen otra información de planta obtenida de de los registros operacionales y de monitoreo de condición. El proceso de modelaje efectúa pruebas de predictibilidad de falla en cada fuente de información disponible. Intenta identificar las variables significativas que influyen en la probabilidad de ocurrencia de los modos de falla de interés.

Los resultados de este enfoque típicamente reducirán el parámetro de forma ß  de Weibull de tal forma que las decisiones basadas en edad gradualmente serán desplazadas (a medida que mejoran los procedimientos de manejo de datos) por decisiones basadas en condiciones. Esta evolución en la  práctica de mantenimiento es deseable debido a que las decisiones basadas en condiciones tienden a ser más conservadoras[3] y menos costosas a largo plazo que las decisiones basadas en edad. Testo se debe primordialmente al hecho que las tareas de CBM (cuando son ejecutadas usando un modelo de decisión basado en variables significativas) detectan fallas potenciales mientras que las tareas de mantenimiento preventivo basadas en edad, aun si se ejecutan con excesiva frecuencia, no excluyen totalmente la posibilidad de que algunos ítems sufran de falla funcional. Las consecuencias son costos más altos. La confianza en la predicción de CBM es una función de cuan correlacionadas están las variables de monitoreo de condición con los deterioros de los modos de falla. La existencia de tales correlaciones[4] puede ser determinada de manera más confiable cuando fallas y suspensiones son diferenciadas de manera más exacta en el CMMS.

Los factores de negocios, cuando se combinan con el modelo de riesgo proporcional, producen una gráfica de decisiones óptimas (Figura 3A). la gráfica traza la probabilidad progresiva de falla y de riesgo. “Riesgo” combina tanto probabilidad como costos.  Un punto “transversal” indica el momento óptimo para reparación. El usuario puede establecer sus objetivos optimizadores  en el modelo. Por ejemplo, el objetivo (de una determinada tarea de CBM pertinente a un determinado modo de falla) puede ser establecido para costos, disponibilidad, rentabilidad o una combinación deseada de los anteriores. El método también proporciona un estimativo de vida útil remanente (RUL) y un intervalo de confianza (Figura 3B) independientemente de factores económicos.

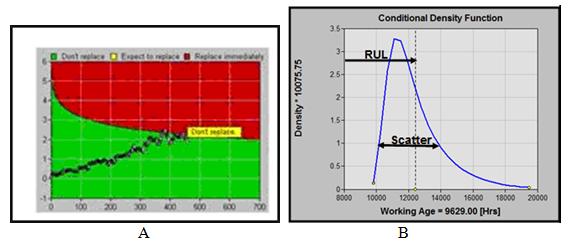
Figura 3A Gráfica de decisión óptima. Eje vertical: la sumatoria ponderada de los valores de cada variable CBM que se ha determinado como significativa en el modelo. Eje horizontal: la edad actual del ítem. Área verde: No acción. Área amarilla (área pequeña entre los límites verde y rojo): Acción requerida en un tiempo especificado. Área roja: Acción recomendada tan pronto sea posible (Ítem se encuentra en estado de “Falla Potencial”). Figura 3B Densidad de Probabilidad Condicional proporciona estimativo de Vida Útil Remanente (RUL) y confianza (desviación estándar) basada solamente en probabilidad.

Un modelo de decisión, como el que se ilustra en la Figura 3, que está basado tanto en costos como probabilidad, identificará el momento más efectivo en costos para intervención (dadas tanto la edad actual de trabajo y los más recientes niveles de las variables significativas monitoreadas).

Los dos requisitos organizacionales más importantes para el modelaje CBM (o para cualquier forma de análisis de confiabilidad basado en información) son:

  1. Que los modos de falla sean bien identificados en las órdenes de trabajo cerradas, y que
  2. Se distinga entre falla (o falla inminente) y reemplazo preventivo (suspensión del ciclo de vida de un componente).

En un análisis de  modelo de riesgo proporcional (PHM), la ecuación de la Figura 4 se resuelve numéricamente.

Figura 4 El modelo Weibull que contiene los parámetros de  forma, ß y de escala, η se extiende mediante un factor exponencial que contiene los parámetros gi asociados con cada variable CBM significativa monitoreada.

A título de ejemplo, el costado derecho de la ecuación PHM en la Figura 4 puede ser \frac{0.781}{2709}\left(\frac{t}{2709} \right)^{0.781-1}e^{0.694*MaxWSDrop+2.49*AccFreezRain} donde (en este ejemplo) el parámetro de forma ß es 0.781 y el parámetro de escala η es 2709 y hay dos variables CBM significativas, MaxWSDrop y AccFreezRain, cuyos parámetros γ1 & γ2 son 0.06944 y 2.49 respectivamente.

El software PHM aplica pruebas estadísticas para el ajuste del modelo y para la importancia de las variables asociadas con los modos de falla y para el apropiado ajuste general de los modelos.

© 2011, Ron Jenkins. All rights reserved.

  1. [1]EXAKT© CBM Decision Optimization ↩
  2. [2]Ver Reference 8.↩
  3. [3]“Más conservador” en el sentido que, debido a que en razón a que CBM (asumiendo que la confianza de detección de CBM es suficientemente alta) detecta fallas “potenciales”, las cuales, por definición, tienen menos consecuencias o consecuencias menores. De aquí que menos fallas funcionales con consecuencias severas se filtrarán.↩
  4. [4]Una suspensión es la renovación de una parte o componente (modo de falla) por cualquier razón diferente a una falla. Si no se diferencia entre falla y suspensión en las órdenes de trabajo cerradas,  no será posible efectuar análisis de confiabilidad basado en información.↩
Articulos similares
Pages: 1 2
This entry was posted in Casos de éxito and tagged , . Bookmark the permalink.