El verdadero significado de las 6 curvas RCM

Posted on mayo 11, 2011 by Luis Hoyos Vásquez

Optimizando TBM – Modelo de costos

Función de densidad

Luego de haber comprendido el método para graficar la relación edad-confiabilidad surge una nueva pregunta: ¿Cómo  el conocimiento de la relación edad-confiabilidad puede ayudar a optimizar el proceso de toma de decisiones del mantenimiento? Lo siguiente  responde la pregunta.

Dos maneras útiles adicionales de expresar la relación de la edad-confiabilidad están expresadas a continuación:

  1. Función de riesgo [1], h(t) 
    1. Esta es la forma usada en los famosos seis patrones de falla RCM (A-F) de la Figura 1 y representada por la ecuación 2.
  2. Función de densidad de probabilidad, f(t)
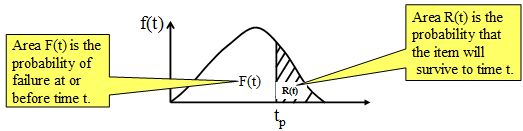
    1. Esta forma, representada por la ecuación 3, tiene algunas características visuales como indicado en la figura 4:
Figure 4 The Probability Density Graph

La conversión entre las funciones de riesgo y densidad de probabilidad es alcanzada a través de la relación:

h(t)=f(t)/R(t).

Mientras el valor de la función de densidad , f(t), no contenga ningún [2] significado físico en el área bajo la curva, F(t), es conocida como la probabilidad  de falla antes de lograr una edad específica t. Inversamente, el área sombreada, R(t), es la probabilidad de sobrevivir una misión de duración t. Puesto que éstas son las únicas dos posibilidades, la superficie total debajo de la curva de densidad de probabilidad es unitaria.

Costo esperado

Asumamos que el tiempo tp   es el momento en que por estrategia de mantenimiento preventivo  la renovación del ítem  es llevada a cabo.  Ahora la pregunta  es, “¿Qué valor debe tomar  tp para que sea óptimo?” Por óptimo nos referimos a que los objetivos organizacionales, como por ejemplo  bajos costos operacionales, sean alcanzados. [3] Intentemos responder la pregunta.

Las ecuaciones 8, 9 y 10 expresan y resuelven el problema:

c_{t}=C_{R}R\left(t_{p} \right)+c_{F}\left(1-R\left(t_{p} \right) \right) (Eqn. 8 )

t_{t}=t_{p}R\left(t_{p} \right)+t_{F}\left(1-R\left(t_{p} \right) \right) (Eqn. 9 )

\frac{C_{t}}{t_{t}}=\frac{C_{F}\left(1-R\left(t_{p} \right) \right)}{t_{p}R\left(t_{p} \right)+\int_{0}^{t_{p}}tf\left(t \right)dt} (Eqn. 10[4])

Dónde:
ct es el costo esperado (promedio) de mantenimiento debido a fallas y acciones preventivas.
tt es la edad esperada (promedio) en la que el mantenimiento (ya sea preventivo o como resultado de una falla) se lleva a cabo.
tp es la edad en la que se  va a realizar el mantenimiento planeado. El objetivo del análisis es de optimizar el valor de tp.
tF es tiempo esperado o promedio en que ocurre la falla.
CR es el costo de una acción preventiva.
CF es el costo de una acción correctiva que es mayor que una acción preventiva.
Ct/tt en la Eqn 10 es el costo de mantenimiento a largo plazo (falla y preventivo).

La ecuación 8 puede leerse:

El costo de operación esperado, para el promedio de ciclo de vida (ct), es igual al costo de una reparación preventiva (cR ) multiplicada por la probabilidad que un ítem sobreviva hasta( tp ) más el costo de reparación de falla (cF ) multiplicado por la probabilidad que el ítem no vaya a sobrevivir hasta (tp).

Una declaración similar se puede hacer para el tiempo esperado de mantenimiento tt, expresado en la ecuación 9.

El gerente de mantenimiento generalmente está interesado en minimizar el costo total esperado por unidad de mantenimiento y reparación de un ítem.  Este es expresado por la relación ct/tt, en la Eqn. 10. La ecuación 10 expresa el costo del mantenimiento de un ítem en relación con su “unidad” de uso.  La ecuación 10 puede ser “solucionada” numéricamente para el valor de tp, minimizando el costo de mantenimiento a largo plazo. El software encuentra el tp  el cual minimiza [5] a largo plazo el costo de mantenimiento por unidad de trabajo Ct/tt .

Conclusión

En este artículo se describe el razonamiento detrás de los seis patrones de falla que Nowlan & Heap revelaron al mundo en su trabajo fundamental. Su informe, titulado “Reliability Centered Maintenance”, fue presentado el 31 de diciembre  de 1978 al Secretario de Defensa de los Estados Unidos. La importancia del RCM no debe ser subestimada. Su valor e importancia se extiende más allá del descubrimiento de los 6 patrones de falla de la figura 1. Nowlan & Heap demostraron que el mantenimiento efectivo solo puede lograrse cuando el departamento de mantenimiento destina todos los modos de falla en medida proporcional a su probabilidad de ocurrencia y sus consecuencias.  Un primer análisis RCM es  llevado a cabo por personas con experiencia en base a su conocimiento y memoria sobre la falla de un ítem. Nowlan & Heap señalaron, sin embargo, que el análisis RCM aun cuando es conducido por personal capacitado, es imperfecto y tendería a ser excesivamente conservador. El conocimiento RCM debe ser continuamente revisado y refinado. El RCM Viviente (LRCM) actualiza el análisis RCM mediante la evaluación repetida de los datos asociados de mantenimiento. El proceso LRCM asegura que el Análisis de Confiabilidad (RA), en particular cuando se aplica en la optimización del Mantenimiento Basado en la Condición (CBM), se beneficie de buena información y de buenos métodos de manejo de datos. Los técnicos, ingenieros y gerentes, utilizando los procedimientos LRCM, mediante un proceso continuo mejorarán la base de conocimiento RCM, refinarán la estrategia de mantenimiento y aumentarán el desempeño del mantenimiento.

© 2011, Luis Hoyos Vásquez. All rights reserved.

  1. [1] La función de riesgo es también conocida como “función de rata de falla ” o “probabilidad condicional de falla”. Es la probabilidad de falla en el próximo intervalo corto de tiempo (considerando que el ítem ha sobrevivido en el inicio de ese intervalo).  Una historia acerca de la función de riesgo contada por John Moubray puede ser vista aqui.↩
  2. [2]Podemos considerar la “densidad de probabilidad” como la “probabilidad de falla por unidad de edad”.↩
  3. [3]El objetivo también puede especificar “disponibilidad más alta posible” o una mezcla óptima de alta disponibilidad, alta confiabilidad y bajo costo.↩
  4. [4] La derivación del denominador de la Eqn 10 puede encontrarse aqui.↩
  5. [5] El objetivo puede de igual manera ser especificado como “disponibilidad máxima” o una combinación deseada de disponibilidad y confiabilidad alta y “efectiva”.↩
Articulos similares
Pages: 1 2 3
This entry was posted in RCM, Teoría y definiciones and tagged , , , . Bookmark the permalink.