El verdadero significado de las 6 curvas RCM

Posted on mayo 11, 2011 by Luis Hoyos Vásquez

Estimación de Parámetros utilizando la regresión

Las siguientes ecuaciones para estimar los parámetros de Weibull están explicadas  en weibull.com.[1] .

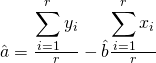\hat{a}=\frac{\displaystyle\sum\limits_{i=1}^r y_{i}}{r}-\hat{b}\frac{\displaystyle\sum\limits_{i=1}^r x_{i}}{r} (Eqn. 5)

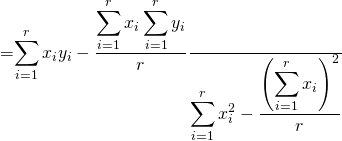$\hat{b}=\frac{\displaystyle\sum\limits_{i=1}^{r}x_{i}y_{i}-\frac{\displaystyle\sum\limits_{i=1}^{r}x_{i}\displaystyle\sum\limits_{i=1}^{r}y_{i}}{r}}{\displaystyle\sum\limits_{i=1}^{r}x_{i}^{2}-\frac{\left(\displaystyle\sum\limits_{i=1}^{r}x_{i} \right)^{2}}{r}}{}$ (Eqn. 6)

x_{i}=ln\left[T_{i} \right] and y_{i}=ln\left[-ln\left[1-F(T_{i}) \right] \right] (Eqns. 7)

Dónde:
^ indica que el valor es una estimación.
Cada F(Ti) se obtiene  mediante los Rangos Medios o la Formula de Bernard.
N= Número de Observaciones.
r(≤N)=Número de Fallas.
i es el número de orden secuencial de cada falla ajustada para las suspensiones como se describirá en la siguiente sección.

Una vez el algoritmo del computador ha estimado a y b de las ecuaciones 5, 6 y 7, los valores de β y η pueden ser encontrados fácilmente a partir de a = –βln[η] y  b=β. Ahora cualquiera de las curvas de las ecuaciones 1, 2 o 3 pueden ser graficadas y examinadas para entender el comportamiento de falla del ítem basado en la edad.

Suspensiones

Orden

Ahora que ya hemos discutido, en términos generales, el método Weibull para graficar la relación edad – confiabilidad (usando históricos de datos de falla), dirigimos nuestra atención a los datos de “suspensiones”, el cuál es el tema principal de este artículo. Comencemos con la muestra de ciclos de vida de la tabla 2:

Tabla 2
Item Edad de Falla Orden
A 84 semanas 1
B 91 semanas 2
C 122 semanas 3
D 274 semanas 4

Los ítems están organizados en secuencia según sus tiempos de supervivencia.  N es el número total de observaciones, en este caso 4 y “i” es el orden (1,2,3 o 4) de una observación de falla. Podemos fácilmente utilizar la fórmula de Bernard para calcular el CDF de cada una de las 4 observaciones.  Luego procedemos, según los métodos  discutidos anteriormente, a determinar  los parámetros Weibull y de ese modo la relación edad – confiabilidad.

Orden con suspensiones

Tomemos como ejemplo que el ítem B, no falló pero fue renovado según lo planeado en los planes de mantenimiento preventivo. En tal caso, ¿Cuál sería el orden (de falla) “i” para utilizar en la fórmula de Bernard? En este caso no conocemos más el orden de falla porque no sabemos exactamente cuándo (después de la semana 91) el ítem B habría fallado si no hubiera sido remplazado preventivamente.

Tabla 3
Item Falla (F#) o Suspensión (S#) Edad de falla o de suspensión Orden
A F1 84 semanas 1
B S1 91 semanas  
C F2 122 semanas ?
D F3 274 semanas ?

La tabla muestra que la primera falla fue a las 84 semanas. Luego a las 91 semanas un ítem fue puesto fuera de servicio por razones diferentes a una falla. Es decir, su ciclo de vida fue “suspendido” (S). Dos fallas más ocurrieron en las semanas 122 y 274. El orden real de las fallas C y D es desconocido debido  a que  depende de cuando B habría fallado. Por lo tanto, sus órdenes son indicados con “?”.

Usando órdenes promedio

Los datos de suspensión son manejados asignando un número promedio de orden para cada falla. El “promedio” es calculado al considerar todas las posibles secuencias:

Si la parte suspendida fallará existen tres escenarios posibles (dependiendo de cuando hubiera fallado el ítem B si este no hubiera sido suspendido). En cada uno de estos escenarios la falla hipotética del ítem B es identificada por “S1 ->F” en la tabla 4

Tabla 4
Escenarios posibles i=1 i=2 i=3 i=4
Posibilidad 1 F1 S1-> F F2 F3
Posibilidad 2 F1 F2 S1->F F3
Posibilidad 3 F1 F2 F3 S1->F

Dónde:
F1 representa la primera falla del ítem,
F2 representa la segunda falla del ítem,
F3 representa la tercera falla del ítem,
S1 representa la primera (y única) suspensión del ítem en esta muestra. 

La primera falla observada (F1) tendrá siempre la primera posición y el orden i=1. Sin embargo, para la segunda falla (F2)  existen dos escenarios de tres donde puede estar en la posición 2 (orden i=2) y un camino en donde puede estar en la posición 3 (orden i=3). De este modo, el orden promedio para la segunda falla es:

\frac{3 \times1+2 \times 2}{3}=2.33

Para la tercera falla (F3)existen dos maneras para estar en la posición 4 (orden  i=4) y una para estar en la posición 3 (orden i=3)

\frac{4 \times 2+3 \times 1}{3}=3.67

Usaremos estos valores  promedios de posición para calcular el rango medio de la fórmula de Bernard (valores mostrados en la columna 5 de la tabla 5) para usarlos en las ecuaciones 4 y 5.

Nuevo incremento

Tabla 5
Item Falla o Suspensión Edad de falla o suspensión Orden, i Rango Medio
A F 84 semanas 1 0.16
B S 91 semanas ?  
C F 122 semanas 2.33 0.46
D F 274 semanas 3.67 0.77

Obviamente, hallar todas estas secuencias para una mezcla de varias suspensiones y fallas y luego calcular los números de orden promedio es un proceso que lleva mucho tiempo. Afortunadamente una fórmula está disponible para calcular el orden. La fórmula produce un “nuevo incremento”. El nuevo incremento “I” está dado por:

I=\frac{\left(n+1 \right)-\left(previous \;order \; number \right)}{1+number \;of\; items\; following\; the\; suspended\; set}

Donde
n= el número total de  ítems en la muestra.
I= el incremento

Entonces para las fallas en las semanas 122 y 274 el incremento será de:

I=\frac{\left(4+1 \right)-\left(1 \right)}{1+2}=1.33

El incremento  seguirá siendo 1.33 hasta la siguiente suspensión, donde será recalculada y utilizada para las fallas posteriores. Este proceso es repetido para cada conjunto de fallas seguidas por cada conjunto de suspensiones. El número de orden de cada falla se obtiene al sumar el “incremento” de la falla al número de orden de la falla previa. Por ejemplo, en la tabla 5 el orden del Item C (2.33)  es 1+1.33, y el Orden del item D (3.67) es aproximadamente 2.33+1.33.

Ahora que tenemos calculadas las ordenes i para cada una de las fallas, podemos proporcionar las F(t)’s [2] requeridas por la ecuación 7 para estimar, utilizando la regresión, los parámetros de Weibull.

Software

Figure 3 Analysis selection in SimuMatic

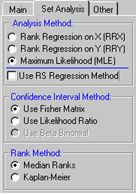
Aunque  lo anterior parezca complicado,  la eficiencia  y el poder del software de confiabilidad convierten el trabajo demasiado fácil.  Por ejemplo, con la herramienta de Reliasoft, SimuMatic, se requiere simplemente que el usuario importe los datos y seleccione el método de cálculo deseado. (Vea la figura 3)

La Figura implica que hay varios métodos alternativos del cálculo que se pueden utilizar para estimar la relación de edad-confiabilidad. Hemos brevemente descrito uno de ellos, el Método de los Mínimos Cuadrados con rangos medios. Otro método popular es conocido como la Estimación por Máxima Verosimilitud (MLE)[3]. Este artículo proporciono conocimiento sobre los seis famosos patrones de falla RCM (mostrados en la figura de la introducción de este artículo) y sobre la pregunta: ¿Cómo hallar la verdadera relación edad-confiabilidad desde muestras reales conteniendo vidas suspendidas? En la siguiente y última página se aborda  la combinación entre la relación de edad-confiabilidad con factores del negocio con el fin de establecer un intervalo óptimo de mantenimiento preventivo.   

© 2011, Luis Hoyos Vásquez. All rights reserved.

  1. [1]http://www.weibull.com/LifeDataWeb/estimation_of_the_weibull_parameter.htm. La única diferencia siendo que la Eqn. 5 y 6 representan la posibilidad de suspensiones de vida N-r las cuales son comunes en mantenimiento.↩
  2. [2]a partir de las Tablas de Rangos Medios o de la Formula de Bernard↩
  3. [3]Para mayor información sobre el MLE ver http://www.omdec.com/wiki/tiki-index.php?page=maintenanceStatistics4 ↩
Articulos similares
Pages: 1 2 3
This entry was posted in RCM, Teoría y definiciones and tagged , , , . Bookmark the permalink.