El Elusivo Intervalo P-F

Decisiones CBM basadas en economía y en probabilidad

Negocios exitosos enfrentados a una diversidad de factores de riesgo optimizan sus políticas y recursos con el fin de alcanzar sus objetivos finales. Un modelo de decisión económica es una regla para la renovación preventiva de un activo, que minimiza el costo promedio por unidad asociado con mantenimiento (proactivo y reactivo) para un horizonte a largo plazo. (Este costo es el indicador de desempeño clave mas directamente relacionado con valor para los accionistas.) Este tipo de regla para CBM puede ser expresado de manera razonable como una política de límite de control: efectuar mantenimiento preventivo en T_d, if T_d < T; o efectuar mantenimiento reactivo en T si T_d ≥ T, donde

T_d=inf{t≥0:Kh(t,Z^(d)(t))≥d} (eq. 10)

K es la penalización en costo asociada con falla funcional, h(t,Z^(d)(t) es el riesgo, y d (> 0) es el límite de control para efectuar mantenimiento preventivo. Aquí el riesgo es definido como la penalización en costo por falla funcional K por la rata de riesgo.

El costo esperado de mantenimiento al largo plazo (preventivo and reactivo) por unidad de edad de trabajo será

(eq. 11)

donde C_p es el costo del mantenimiento preventivo, C_f = C_p+K es el costo del mantenimiento reactivo, Q(d)=P(T_d≥T) es la probabilidad de falla previa a la acción preventiva, W(d)=E(min{T_d,T})) es el tiempo esperado de mantenimiento (preventivo o reactivo).

Dejemos que d* sea el valor de d que minimiza el costado derecho de la Ecuación 11. Corresponde a T* = T_d*. Makis y Jardine en  ref. 3 han mostrado que para una función de riesgo que no disminuye h(t,Z^(d)(t), la regla T* es la mejor de todas las políticas de reemplazo (ref. 4).

Let d* be the value of d that minimizes the right-hand side of Equation 11. It corresponds to T* = T_d*. Makis and Jardine in ref. 3 have shown that for a non-decreasing hazard function h(t,Z^(d)(t), rule T* is the best possible replacement policy (ref. 4).

La ecuación 10 puede ser re-planteada para la política óptima de límite de control así:

T*=T_d*=inf{t≥0:Kh(t,Z^(d)(t))≥d*} (eq. 12)

Para el modelo PHM con la distribución base de Weibull, puede ser interpretada como (ref. 2))

(eq. 13)

donde  (eq. 14)

Ref. 2 menciona la solución numérica para la Ecuación 13, que es descrita en detalle en(Ref. 7) y en (Ref. 8). La función

g(t)=δ^*-(β-1)ln(t) (eq. 15)

es la función del “nivel de advertencia” del ítem reflejado por la suma ponderada de valores actuales de las variables CM significativas (covariables). Un gráfico de función versus edad de trabajo puede ser considerado como un cuadro de decisión económica que muestra si la información sugiere que el ítem debe ser reemplazado. En el cuadro de decisión, aproximamos el valor de by

Un ejemplo de un cuadro de decisión con varios puntos de inspección puede ser encontrado en la Figura 3. Estudios de caso detallados, basados en el modelo comentado en esta sección se pueden encontrar en ref. 5 y en (ref. 6).

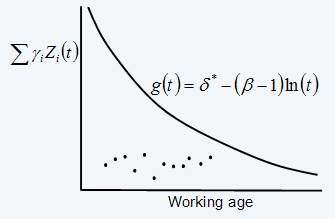
Figura 3: Muestra de cuadro de decisión económica (para ß>1 )

El anterior desarrollo de (ref. 2) habla a costos como el objetivo optimizador. Desarrollos análogos se han hecho en EXAKT tomando en consideración la disponibilidad y la rentabilidad como los objetivos optimizadores. Para estos dos objetivos solamente necesitamos cambiar la función de objetivo en la Ecuación 11 de manera acorde.

Específicamente, para el objetivo de disponibilidad, la Ecuación 11 será reemplazada por la función de disponibilidad, definida como la proporción de tiempo de funcionamiento al tiempo de funcionamiento mas el tiempo de parada.

(Ec. 16)

donde W(d) es el tiempo de funcionamiento esperado, tp es el tiempo de parada como resultado de mantenimientos planeados y tf es el tiempo de parada como resultado de mantenimientos forzados por una falla funcional. El objetivo también ha sido cambiado para maximizar aΦ(d), Ej., d* será el valor que minimice el costado derecho de la Ecuación 16.

Para el objetivo de rentabilidad, la Ecuación 11 será reemplazada por la función de costo global

(Ec. 17)

donde a_p es el costo por hora del tiempo de parada planeado y af es el costo por hora de tiempo de parada no-planeado. El objetivo es minimizar la Ecuación 17, Ej., encontrar a d*, que es el valor de d que minimiza el costado derecho de la Ecuación 17.

© 2011 – 2012, Luis Hoyos Vásquez. All rights reserved.