El Elusivo Intervalo P-F

Abstract

En este artículo se analiza el Intervalo P-F para la toma de decisiones CBM, sus áreas de utilidad y aquellas áreas en las que es inadecuado utilizarlo como estrategia de mantenimiento predictivo. Proponemos un enfoque alternativo más general basado en el sistema EXAKT. Se describen dos categorías de decisiones, la primera basada en la probabilidad de falla, y la segunda basada en la probabilidad de falla y aspectos económicos. Bajo la segunda categoría existen tres posibles estrategias de decisión: minimización de costos, maximización de disponibilidad, y maximización de rentabilidad (considerando tanto costos como disponibilidad). Un ejemplo numérico ilustra estos cuatro tipos de decisiones. Referencias (Ej. los hipervínculos en las etiquetas de las ecuaciones 4, 6, 10, y 11) al Apéndice proporcionan clarificación adicional donde se necesite.

Antecedentes

Cuando la capacidad funcional de un equipo cae por debajo de su capacidad requerida, consideramos que el activo ha “fallado”. Mantenimiento restaura (mantenimiento reactivo), o conserva (mantenimiento proactivo) la capacidad funcional de un ítem a un nivel que excede aquel requerido por sus usuarios. De los dos tipos de mantenimiento, reactivo ó proactivo, en ciertas situaciones los usuarios especifican este último en ciertas situaciones. En aquellos casos en que la falla pueda interferir de manera significativa con el nivel de alistamiento en un contexto militar, o con la meta de producción de bienes y servicios, con la seguridad industrial, con rentabilidad y sin violar las normas ambientales, por lo general el usuario solicitará algún tipo de mantenimiento proactivo.

Con el fin de mitigar las consecuencias de fallas, los administradores de mantenimiento se inclinan hacia una política de mantenimiento denominada mantenimiento basado en condiciones o CBM. CBM es también conocido (con diversos matices), con los nombres “mantenimiento basado en condición”, “mantenimiento predictivo” (PdM), “monitoreo de condiciones” (CM), “administración de pronósticos & salud” (PHM), “monitoreo de salud de equipos” (EHM), o simplemente como “inspecciones de mantenimiento preventivo (PM)”

Todas estas se refieren a la recolección, el procesamiento y el análisis de información y observaciones relevantes, con el fin de tomar decisiones buenas y oportunas sobre:

1. Intervenir inmediatamente y hacer mantenimiento a el equipo en este momento, o
2. Planear la ejecución de un mantenimiento dentro de un periodo de tiempo especificado, o
3. Aplazar la decisión de mantenimiento hasta la próxima observación CBM.

Cuando los administradores y los gerentes seleccionan una tarea para tratar un particular modo de falla, tienden a considerar a CBM en primer lugar. CBM, de ser aplicable, es considerado como mas “conservador”, menos costoso, y menos entorpecedor que TBM (mantenimiento basado en tiempo). El gráfico de la Figura 1 representa la conocida teoría de CBM. Define a CBM como la detección de una falla potencial de manera oportuna. P es el punto inicial en el cual puede ser observada una falla en evolución, utilizando la tecnología actual de detección. El real descubrimiento de la falla potencial ocurre en la siguiente inspección CBM después de P.

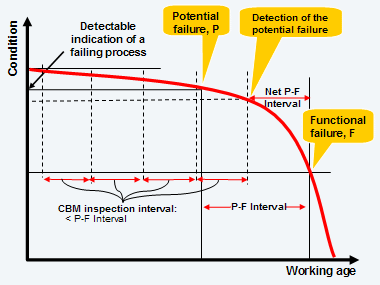
Figura 1 El modelo clásico CBM

Discusión

El gráfico en la Figura 1 a la izquierda, ilustra las restricciones que debe tener en cuenta el ingeniero de mantenimiento al diseñar un programa CBM. El intervalo P-F Neto debe proporcionar un periodo de tiempo adecuado para que la operación de mantenimiento reaccione a partir del momento en que es detectada una falla potencial. Si resulta práctico monitorear a la frecuencia necesaria para que esto ocurra, el programa CBM se considera como “técnicamente factible” o “aplicable”. En el peor de los casos, según el gráfico, si una inspección anticipa la falla potencial solamente por un pequeño periodo de tiempo, la siguiente inspección todavía la detectará a tiempo, siempre y cuando la organización de mantenimiento sea capaz de actuar dentro del intervalo P-F neto. En caso que, al largo plazo, la tarea proactiva repetitiva tenga éxito, a un costo aceptable, en evitar o mitigar las consecuencias de fallas funcionales, se considerará que el programa CBM es “efectivo” o que “vale la pena”.

La Figura asume que:

1. El punto en el que se declara una falla potencial, P, de una condición identificable es conocido, y que
2. El intervalo P-F es conocido y es razonablemente consistente (o su rango de variación puede ser estimado), y que
3. Resulta práctico monitorear el ítem a a intervalos mas cortos que el intervalo P-F.

El modelo clásico de decisión CBM de la Figura 1 depende considerablemente, por lo tanto, de conocimiento previo sobre P y del intervalo P-F. en la práctica RCM, se obtiene una aproximación inicial al Intervalo P-F mediante el consenso de expertos en el tema (ref. 1).

Obstáculos para la aplicación de la Figura 1

Moubray, en ref. 1, sugiere que si P no es conocido, o que si P-F no puede ser aproximado, CBM no es técnicamente viable. Esto descartaría un gran número de programas de monitoreo de condición actualmente activos. De los dos conceptos, “P” y “P-F”, es el primero el que presenta el reto más grande. Sin “P” el intervalo P-F resulta elusivo. Por esto, antes de tratar el intervalo P-F, debemos primero descubrir cuando y como declarar una falla potencial.

En la Figura 1, “P” (el punto en el cual la tecnología actualmente disponible puede detectar una condición de falla) es señalizado cuando se alcanza un valor especificado para algún indicador de condición. Encontrar un indicador que trasmita el estado de un modo de falla fijado es un reto por sí mismo. En todas las situaciones, excepto las más simples, extraer un indicador de condición (característica) que de una manera fiel haga seguimiento a resistencia de falla disminuyente, relacionada con un modo de falla objetivo, (también conocido como causa o mecanismo), requiere de considerable conocimiento, basado en:

1. Un modelo de ingeniería del mecanismo de falla, o en
2. Experiencia previa de la falla o, preferiblemente, de la falla potencial.

En la presente discusión, asumiremos que no hay disponible un modelo basado en reglas físicas. Nos enfocaremos en el segundo caso, que se podría considerar como el más general. Una vez se haya propuesto un indicador de condición que refleje el deterioro en un componente, todavía nos toca establecer el punto de decisión P (falla potencial) en el cual, ante la falta de un  modelo que describa las reglas de física del modo de falla, se requiera de alguna clase de metodología.

Esto (establecer el nivel al cual se declara la falla potencial) es el problema encontrado por muchos administradores de activos agobiados por información de monitoreo de condición. La persona que implementa un programa CBM enfrenta interrogantes inevitables. Estos son, “Donde establecer la falla potencial?”, y, “Cual indicador, de las tantas variables monitoreadas, debería utilizar para este propósito?” Cuando las reglas físicas de una situación no son bien conocidas (como es el caso muy frecuentemente), una “política” para declarar una falla potencial no es nada obvia.

Por qué la Figura 1 y la determinación de P y de P-F nos resultan tan elusivas? Las razones son:

1. Si bien ello no implica esto, podemos erróneamente inferir a partir del gráfico en la Figura 1 que, en general, un solo indicador de condición influye sobre la probabilidad de falla. Sin embargo, frecuentemente el problema es multi-dimensional. Cuando una variable significativa es una combinación lineal de varios factores que influyen sobre riesgos, se trata de una función más compleja que, por lo general, no es fácil de forzar en el modelo P-F simple.
2. P y P-F pueden ser variables aleatorias. Los intentos de establecer estas como parámetros fijos de decisión frecuentemente nos causan frustración.
3. La declaración de P puede no ser constante para diversas edades de trabajo del ítem. Un alto nivel de vibración en un ítem más antiguo puede indicar una falla inminente mientras que el mismo nivel de vibración en un ítem más nuevo puede ser normal. En general necesitamos un método para determinar la relación tripartita (edad vs. Indicador CBM Indicador vs. confiabilidad).
4. (reproducidos a continuación) tratan dos casos extremos. En el primer caso (“Caso Especial 1? a continuación), conocido como comportamiento aleatorio, no existe relación entre la probabilidad de falla Y EDAD. (F1, F2, F3 ocurrieron en edades aleatorias) en el segundo (“Caso Especial 2?), la falla depende totalmente de la edad. En los siguientes tres párrafos se discuten las confusiones que pueden surgir a raíz de generalizaciones de estos casos especiales.
   1. Ref. 1 describe de manera correcta el primer caso como una situación en la cual la probabilidad condicional de falla depende totalmente de un indicador de condición y es
      

      Casos especiales CBM

      Completamente independiente de edad.

   2. En el segundo caso surge una confusión, donde ref. 1 igualmente indica que la falla depende del indicador de condición. Sin embargo, Ref. 1 no menciona que el indicador de condición (en este caso, la profundidad del surco en una llanta) es una variable que es equivalente a la edad del componente. Este tipo de indicador es, en este caso simplista, una medición directa de la tensión externa acumulada, que es la “edad de trabajo”. De hecho, falla es frecuentemente definida directamente en términos de esta medición. Por ejemplo cuando la profundidad de surco de una llanta de avión llega a un valor mínimo especificado, se le considera en falla debido a que ya no puede mantener la función de la llanta “de ser reencauchada”, en situaciones complejas (generales), el indicador de condición o variable monitoreada, por lo general no es equivalente a la edad de trabajo. Tampoco está, hablando en términos generales, tan obviamente relacionada a falla potencial. Los implementadores de CBM enfrentan el reto de descubrir la relación exacta entre la información relevante de monitoreo de condición y la probabilidad de supervivencia.
   3. En la práctica, la falla frecuentemente depende de edad y de uno o varios otros indicadores de condición adicionales. (Podríamos considerar la dependencia de la edad como un promedio de una multitud de otros factores indeterminados.) Para este caso general, se requieren metodologías mas avanzadas con las cuales revelar la falla potencial y determinar el intervalo P-F.

Toma de decisiones CBM en EXAKT

EXAKT maneja la multi-dimensionalidad de CBM, la naturaleza probabilista de la falla y la influencia de la edad de trabajo, proporcionando dos maneras de decidir si un ítem, componente, o  modo de falla se encuentra en estado de falla potencial. Adicionalmente, si el ítem no se encuentra actualmente en estado “P”, EXAKT de todas maneras proporciona un tiempo estimado para la falla o un estimativo de vida útil remanente (RULE). Los dos procesos de decisión se pueden categorizar como:

1. Una decisión basada en la combinación de probabilidad de falla y las consecuencias cuantificables de la falla, y
2. Una decisión basada solamente en la probabilidad de falla.

La primera estrategia CBM de toma de decisiones proporcionará soporte a decisiones relacionadas con las consecuencias operacionales y no – operacionales de la falla cuyo impacto económico puede ser estimado, por ejemplo, la falla de un componente en una línea de producción. El segundo método se aplicará a decisiones que deben ser basadas estrictamente en probabilidad. Estas incluyen situaciones fuera de lo esperado, cuyos costos de falla son desconocidos o incalculables, tales como aquellas en que se involucren consecuencias ambientales, de salud y de seguridad de naturaleza catastrófica. Los administradores utilizan ambos tipos de método de decisión de manera regular dentro del alcance de sus responsabilidades. El flujograma de la Figura 2 resume la funcionalidad de EXAKT en estos dos procesos de decisión.

Figura 2: Flujograma de EXAKT. La información acerca de edad es también conocida como información de “vida”, y está compuesta por la edad de trabajo y el tipo de evento (falla o suspensión) definiendo cada terminación de vida. La información CM es información de “monitoreo de condición”. La “información de Costos” define la “penalización”, o costo promedio asociado con la falla, comparado con el costo promedio de prevenir la falla.

La mayoría de decisiones en mantenimiento son basadas no solamente por consideraciones sobre la probabilidad de supervivencia del activo, sino también por factores económicos.

En lo que respecta a la dinámica del negocio, los  administradores rápidamente logran apreciar la necesidad de optimizar sus decisiones respecto a objetivos conflictivos. Una política es un procedimiento (modelo) para tomar las mejores decisiones teniendo en consideración las evidencias disponibles en ese momento. Obtener valor a partir de nuestra política de decisiones depende de:

1. Tener la información correcta, y
2. Transformar esa información en el curso de acción.

El ingeniero de mantenimiento y su gerente deben, por lo tanto, comprender y estar de acuerdo respecto al significado del término “mejor” dentro del actual contexto de operación. Para definir “confiabilidad” en el sentido general de la palabra (no en el sentido matemático), podríamos decir que es: Alcanzar la rata de producción, calidad, disponibilidad, supervivencia de la misión, deseadas, al costo más bajo, de manera segura y sin infringir normas ambientales.

Los siete elementos deseables: 1. Rata de producción, 2. calidad, 3. Disponibilidad, 4. Supervivencia de la misión, 5 Costos más bajos. , 6. Seguridad, 7. Integridad ambiental, raramente son mutuamente inclusivos. Por lo general están en conflicto. Si giramos el botón de velocidad en la  rata de producción, esto podría afectar adversamente la calidad (rendimiento  final). Si operamos los equipos hasta cuando fallen, podríamos obtener una disponibilidad aceptable, pero se podrían incrementar los costos. Y así sucesivamente.

Las posibilidades entre estos objetivos son interminables. En razón a la inmensa variedad de resultados de un proceso de decisión, no resulta sorprendente que los departamentos de mantenimiento se esfuercen en establecer con exactitud el punto central de la elusiva “confiabilidad”. Al enfrentar objetivos conflictivos, los administradores reconocen la necesidad de llegar a un compromiso.

Los compromisos en mantenimiento nos conducen directamente al tópico de optimización. El proceso de optimización EXAKT ayuda a reducir una diversidad de objetivos a un denominador común, de modo que el proceso de optimización produzca la mejor solución de compromiso entre varias metas. En el ejemplo numérico a continuación, mostramos la manera en la cual EXAKT equilibra los objetivos de bajos costos y alta disponibilidad en una política CBM optimizada. Pero antes, comentemos acerca del tema de optimización con respecto al objetivo de costos.

En general, ni P ni F ocurren a tiempos fijos ni bajo condiciones fijas. Más bien, ocurren de manera aleatoria de acuerdo con distribuciones de probabilidad. EXAKT es un enfoque probabilístico que decide, basado en la condición actual con relación a un óptimo nivel de riesgo, si es que se requiere de mantenimiento. La diferencia de enfoques será explorada en este artículo. En mantenimiento, la incertidumbre respecto al tiempo cuando ocurrirá la falla es la realidad. La creciente temperatura de un rodamiento, una presión diferencial incrementándose de manera linear en un filtro, o los surcos de las llantas de una aeronave desgastándose de manera proporcional al número de aterrizajes, son todos casos especiales determinísticos de CBM, caracterizados por estados fijos de P y F. El desarrollo de grietas en un componente mecánico es más estocástico. El personal de mantenimiento debe adoptar herramientas y procedimientos que traten con los casos generales, los probabilísticos y los casos más frecuentes. Mientras más general, más exactitud.

Pretendemos mostrar de qué manera el problema puede ser tratado de manera más clara solamente cuando este es enfocado de manera estadística. Hablaremos acerca de manejar la incertidumbre con el  fin de presentar un argumento fuerte respecto a como el enfoque simplificado o aproximado (intervalo P-F) no conducirá, por lo general, a resultados que traten de manera realística con los cambios en la resistencia a falla.

© 2011 – 2012, Luis Hoyos Vásquez. All rights reserved.