El artículo que describe la optimización CBM en EXAKT, “The Elusive P-F Interval”, puede dejar la impresión de que el intervalo PF es un concepto irrelevante. El intervalo PF no es irrelevante pero si distrae la responsabilidad más importante del diseñador de un programa CBM que debería ser, la detección confiable de “P”.
De NAVAIR 00-25-403 el intervalo CBM es I =PF/n donde “n” dependerá de:
- La probabilidad, θ, de detectar una falla potencial con una ocurrencia de la tarea CBM propuesta, asumiendo que la falla potencial ha ocurrido
- Probabilidad de falla aceptada (Pacc)
Generalmente, nos enfocamos mucho en el Intervalo PF. Ni Nowlan & Heap ni Moubray tuvieron la intención de utilizar el intervalo PF de forma diferente al de determinar una primera aproximación de un intervalo de inspección CBM en el contexto de un proceso de mejoramiento continuo.
Al enfocarnos en el intervalo PF le restamos valor al mayor desafío de CBM, el de revelar “P”. Una vez se haya adoptado un modelo o una regla para declarar una falla potencial, la evidencia confirmada dentro de las ordenes de trabajo del programa LRCM (ver cinco pasos abajo) proporcionará más información sobre la rata actual de degradación con el fin de afinar el intervalo de inspección.
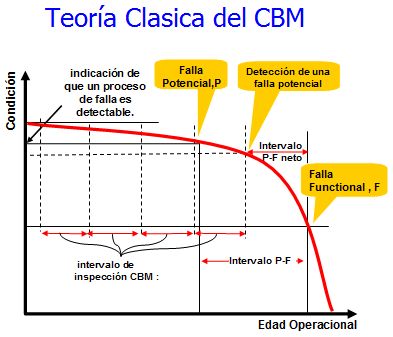
El siguiente gráfico explica la teoría “clásica” de CBM:
El “Tiempo de Respuesta” en mantenimiento es el tiempo requerido por el mantenimiento para responder una alerta de “P”. En el peor de los casos, de acuerdo con el gráfico, si una inspección antecede la falla potencial por una pequeña cantidad, la siguiente inspección aún podría detectarla a tiempo, siempre y cuando la organización de mantenimiento sea capaz de actuar dentro del intervalo neto PF.
A partir del gráfico, el intervalo neto PF será siempre mayor que PF/2 (cuando I=PF/2). Si n=3 entonces el intervalo neto PF será mayor que 2PF/3, y así sucesivamente. Por lo tanto debemos elegir un “n” de tal manera que el intervalo neto PF sea mayor que el Tiempo de Respuesta. Cuanto mayor es el valor de “n” usado, se supone que menor es el intervalo de inspección y más costosa será la estrategia de CBM.
El intervalo PF, siendo un modelo simple para explicar CBM, es un tipo de “Catch 22”. Con esto queremos decir que el descubrimiento del intervalo PF requiere la experiencia continua en detectar y reaccionar a “P”. Por otra parte y con el fin de establecer una regla para declarar “P”, necesitamos de la experiencia de haber aplicado y confirmado nuestro modelo PF. El proceso de EXAKT/ LRCM evita esta circularidad con un modelo de Vida Útil Remanente (RUL) que se deriva de los datos CBM y de las ordenes de trabajo relacionadas que representan instancias de modos de falla. El modelo, cuando se aplica día a día, no solo proporciona decisiones prácticas de CBM sino que también mejora la confianza en las predicciones. Con aplicaciones automatizadas de los modelos CBM se obtienen intervalos de confianza de los Estimados de Vida Útil Remanente (RULEs) que soportan y sugieren intervalos de inspección.
En resumen, los ingenieros de confiabilidad deben en primer lugar concentrar sus esfuerzos en la búsqueda de un método claro y confiable para la determinación de “P”. Esto se puede lograr mediante la creación de procedimientos precisos del día a día para observar y registrar fallas y suspensiones en las órdenes de trabajo. Los siguientes pasos describen el proceso LRCM:
- Registrar las fallas y las suspensiones al cerrar las órdenes de trabajo.
- Mejorar continuamente la base de conocimiento RCM al cerrar las órdenes de trabajo.
- Relacionar las órdenes de trabajo a los registros de conocimiento RCM.
- Generar muestras desde el CMMS, basada en la relación órdenes de trabajo – RCM (del paso anterior).
- Ejecutar un análisis CBM y un procedimiento de modelado como EXAKT.
© 2011, Oscar Hoyos Vásquez. All rights reserved.