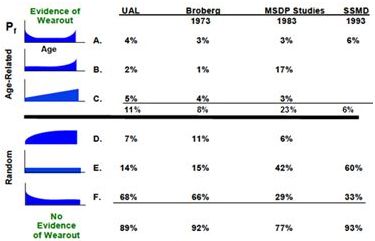
Usted posiblemente está preguntándose por las famosas “curvas RCM” mostradas en la figura 1. Estas son las curvas de comportamiento de Edad-Confiabilidad que grafican la Probabilidad Condicional de falla contra la edad. Una pregunta común es la siguiente.
“¿Representan realmente estas curvas el comportamiento real de falla del ítem para, por ejemplo, los 139 ítems cubiertos por el estudio Nowlan & Heap,? o ¿Representan estas curvas la relación efectiva neta entre edad – confiabilidad, considerando que la mayoría de estos ítems estuvieron sujetos a un mantenimiento periódico?”
Estas son excelentes preguntas. Muchos Ingenieros de Mantenimiento y Confiabilidad no están completamente seguros de la respuesta ni de sus explicaciones correspondientes.
Contents
Introducción
El objetivo de realizar un “análisis de confiabilidad” para trazar estas curvas es el de descubrir el verdadero comportamiento de la falla de un ítem con respecto a cada uno de sus modos de falla significativos [1], sin importar el plan de mantenimiento implementado. ¿Cómo es esto posible? ¿Acaso, no estamos basando nuestro análisis en datos de los equipos que se han mantenido según las actuales estrategias del mantenimiento?
La respuesta es que al momento del mantenimiento (digamos, renovación preventiva de un componente) seguramente hacemos algunas observaciones sobre el estado de los ítems mantenidos. En ese momento es improbable que hayamos observado que todos los ítems renovados estuvieran al borde de la falla. De igual manera, es posible (a menos que el plan de mantenimiento preventivo (PM) sea muy conservador) que algunos ítems hayan fallado antes del momento PM. Es decir, que la falla se haya presentado durante el servicio. Por otra parte, puede que algunos de los ítems renovados no hayan estado en estado de falla al momento PM sino por el contrario, hubieran estado en condiciones excelentes. Finalmente, es posible también encontrar algunos de los ítems a punto de fallar funcionalmente. En este caso podemos considerar el PM como “oportuno”.
Un mantenedor astuto, consciente de las observaciones anteriores, sin duda preguntaría: ¿Cuál es el punto óptimo para conducir el mantenimiento? ¿Qué programa PM (estrategia) tendrá el mayor beneficio?, es decir, ¿cuál nos dará la mejor disponibilidad total sobre la flota a largo plazo? El gerente reconoce que el ser demasiado conservador sería una estrategia poco rentable debido al cambio de componentes en perfecto estado. De la misma manera, tampoco quisiera una estrategia muy liberal al seleccionar intervalos de mantenimiento muy largos. Esto daría lugar a un número excesivo de fallas en servicio, aumentando los costos y reduciendo tanto la confiabilidad como la disponibilidad.
Asumamos que el verdadero comportamiento de la falla es el mostrado en el gráfico de la figura 2, la cual representa el Patrón B de las seis curvas de comportamiento de falla de la figura 1.
La figura 2 gráfica la rata de riesgo o la Probabilidad Condicional de falla [2] contra la edad de trabajo de un ítem. Quisiéramos estar en posición de declarar (a nuestro gerente) que nuestro mantenimiento ha sido optimizado, queriendo decir que fuimos capaces de realizar el mantenimiento a la edad de trabajo representada por la vida útil. La vida útil es el mejor criterio para determinar la realización de un PM. Tal estrategia prevendría la mayoría de las fallas y disminuiría la renovación de componentes que se encuentren en buen estado. Está estrategia conducirá las acciones PM en el momento de máximo beneficio para la organización.
Obviamente, el gráfico de la Figura 2 debe representar la relación inherente entre la edad y la confiabilidad del ítem si intentamos utilizarlo para determinar la vida útil y la estrategia óptima del mantenimiento preventivo. La pregunta es, “¿Cómo graficar esta curva del equipo mantenido con datos reales?”
Los “datos reales” implican que nuestros cálculos deben tener en cuenta los datos de “suspensiones” los cuales reflejan el programa de mantenimiento preventivo en curso.[3] El método estadístico efectivo más popular para describir la relación de confiabilidad y edad está basado en el modelo Weibull para los datos de vida. Este, es un modelo empírico descubierto en los años 1950 por Walodi Weibull, quien presentó la siguiente ecuación ante una distinguida sociedad (que reaccionó en un principio con escepticismo) que luego se convertiría en la sociedad de ingeniería de confiabilidad.
Distribución Weibull – tres de sus formas
Distribución Acumulada (Eqn. 1)
Riesgo (Eqn. 2)
Densidad de Probabilidad (Eqn. 3)
Dónde:
β (beta) es el parámetro de “forma”,
η (eta) es el parámetro de “escala”, y
t es la edad de trabajo del ítem o modo de falla que está siendo modelado.
Para poder graficar la relación confiabilidad – edad (por ejemplo, la Figura 1) solo necesitaremos determinar (calculo a partir de datos históricos) los valores de los parámetros β y η. Estos gráficos nos ayudan a comprender el comportamiento histórico de falla de los componentes y de los modos de falla de interés. Weibull desarrolló un método gráfico para calcular los parámetros β y η de un conjunto histórico de datos de falla. Hoy en día, no necesitamos usar este método gráfico de Weibull ya que existen algoritmos numéricos que calculan los valores β y η y trazan los gráficos requeridos de forma automática.
Ejemplo
Por ejemplo, asuma que tenemos los siguientes ítems idénticos [4] A, B, C, D y E y las edades en las que fallaron.
| Tabla 1: | ||
|---|---|---|
| Item | Edad de falla | Orden[5] |
| A | 67 semanas | 1 |
| B | 120 semanas | 2 |
| C | 130 semanas | 3 |
| D | 220 semanas | 4 |
| E | 290 semanas | 5 |
El ejemplo necesita calcular los valores correspondientes de la Función de distribución Acumulada (CDF) (F(t) en la Ecuación 1) en cada una de las edades de falla 67,120,130,220 y 290 semanas. Es decir, se debe determinar un valor razonable para la fracción de la población que falla antes de la fecha de observación. Esa fracción se aproxima a la probabilidad de falla acumulada (i.e. F(t)) en cada una de las cinco edades de falla “t”.
Necesidad para estimar una mejor Función de Distribución Acumulada (CDF)
No podemos simplemente decir que el porcentaje de falla en 120 semanas es de 2/5 porque eso implicaría que la probabilidad acumulada de falla para 290 semanas es de 100%. Esta muestra pequeña no es suficiente evidencia para afirmar este enunciado.
Para explicar esto de manera más clara consideremos un tamaño de muestra de 1. No se debe esperar que la edad de esta única falla represente la edad de falla del 100% de los ítems de la población de la muestra. Sería , indiscutiblemente, más realista considerar que esta edad única de falla representará la edad a la que el 50% de la población podría fallar.
Según lo anterior, es claro que necesitamos una mejor manera de calcular la CDF, especialmente para muestras pequeñas de vida, con el fin de poder utilizarla en la solución numérica de Weibull para graficar la relación edad – confiabilidad. La propuesta más conocida para calcular la CDF a partir de los datos de falla se conoce como rango medio. [6] La fórmula, conocida como “estimador de probabilidad de Bernard”, proporciona un cálculo de rango medio para muestras pequeñas y está descrita por la Ecuación 4.
Estimador de Probabilidad de Bernard
![]() (Eqn. 4)
(Eqn. 4)
Dónde:
i= el orden secuencial de la falla; y
N= el tamaño de la muestra (número de ciclos de vida)
Estimado CDF = El estimado de la Función Acumulada de Distribución o rango medio.
La fórmula de Bernard, empleada en nuestro caso hipotético de única falla, da (1-0.3)/ (1+0.4) =50%, lo cual es intuitivamente razonable.
Obtenemos, ya sea de las tablas de rangos medios o de la aproximación de Bernard, las probabilidades acumuladas de falla respectivas (i.e las CDFs). Estas son 0.13, 0.31, 0.5, 0.69, y 0.87. Por supuesto que cuando usamos software de análisis de confiabilidad no es necesario buscar manualmente las tablas de rangos medio o la fórmula de Bernand. Un programa de computadora calcula automáticamente [7] los rangos medios de cada observación. El algoritmo emplea una técnica numérica (regresión) conocida como “Método de Mínimos Cuadrados” para calcular los valores de β and η en las siguientes ecuaciones:
© 2011, Luis Hoyos Vásquez. All rights reserved.
- [1] Un modo de falla es el evento que causa la falla. Puede ser definido como la parte, componente o ensamble que falla. Opcionalmente, el modo de falla puede incluir una acción que implique un cambio físico de estado (por ejemplo: caído, atascado, etc.) La expresión del modo de falla también puede terminar con una clausula “debido a” (por ejemplo: fatiga, contaminación, etc.). El nivel de causalidad para describir un modo de falla dependerá de las consecuencias de falla. Las consecuencias más grave necesitan de un análisis más profundo de causalidad y de la exploración de un mayor número de fallas.↩
- [2]La probabilidad condicional de falla es la probabilidad de falla en un próximo intervalo de edad relativamente corto al momento de hacer la pregunta. Es el valor de confiabilidad más importante para la toma diaria de decisiones ↩
- [3]Ver sección de “Suspensiones”↩
- [4] Una objeción legítima plantea la posibilidad de que los ítems de A – E pueden ser idénticos pero operan bajo condiciones o ciclos de trabajo distintos (más o menos duros). El analista debe tener esto en cuenta al seleccionar una medida de edad que no sea el tiempo calendario que normaliza el uso. Por ejemplo: “número de aterrizajes”, “número de rondas”, “litros de combustible consumidos”, etc. Si existen variables, diferentes de la edad, significativas, por ejemplo, datos de monitoreo de condición o de operación, luego el modelo de edad – confiabilidad de Weibull se debe ampliar hasta incluir las medidas de CBM. Dicho método es EXAKT. ↩
- [5]El “orden” es la secuencia según la edad de falla del ítem.↩
- [6]Para mayor información en las tablas y conceptos de Rangos Medios ver http://www.omdec.com/wiki/tiki-index.php?page=maintenanceStatistics4↩
- [7] o utiliza otra estrategia de ajuste de datos, tal como la Estimación de Máxima Verosimilitud (MLE).↩
- EXAKT vs. Weibull (39.8%)
- Garantía para los camiones de carga (26.5%)
- Estándares de declaración de falla (26.5%)
- Optimización de CBM (26.5%)
- Análisis de fallas para análisis de confiabilidad (26.5%)