Ever wonder why poor historical work order data in the CMMS has been tolerated all these decades? One reason is that the fix is a human one. And human behavior is difficult to change. We tend to avoid difficult human problems, ultimately seeking a technological solution to everything. But there’s also a kind of paradox in this business.
Reliability analysis tools are sophisticated. But, as impressive as they are, they are mainly age based. That is, the working age (hours, cycles, widgets produced) is the sole independent variable in the reliability model, for example in the Weibull equation:
![]()
where h(t) is the hazard or failure rate as a function of age t. And β, η are the shape and scale parameters. To use a reliability model we require a “good” sample. A sample is a set records of instances of failure modes, their ages at the time of occurrence, and their respective ending events (either failure, potential failure, or preventive renewal). This information would need to be reported accurately and consistently on the EAM work order, a tall order given maintenance culture and current work order related procedures.
Being age based, the results of Weibull analysis performed in a maintenance department are usually vague since the age variable averages (i.e. obscures) a mixture of other more relevant factors such as overload frequency, temperature spikes, oil debris, and so on. The results of the purely age based analysis are often of little usefulness in day to day practical maintenance decisions. That being the case, erratic and imprecise failure codes reported on the work order are seldom a pressing problem for today’s maintenance engineers. Although they occasionally complain about EAM data inconsistency and inaccuracy, they devote much of their attention to relatively easy-to-acquire condition data in which they try to discover predictive content.
Good work order data only becomes important (i.e. bad age data becomes glaringly obvious) when one attempts to correlate it with relevant condition monitoring (CM) data using an extended form of reliability analysis.[1] In other words we need good work order data to discover the predictive content of our condition monitoring data. If we don’t use CM data in an analytic evidence based process, we will never have to confront the inadequacy of our EAM work order data. That’s the “Catch 22”[2]. Since CBM data is relatively easy to acquire human nature and the path of least resistance encourage the purchase of more sensor related technology from which we hope, in a Eureka moment, to find predictive clarity.
A more systematic approach would exploit the ability of the EAM to track working age accurately and to generate samples for reliability analysis. Correlating age and condition data would reveal which condition data patterns precede failure. The Mesh Living RCM (LRCM) system brings age data into the predictive model by means of its two principal functions:
- To ensure perfect transcription of technician observations into the EAM database as analyzable data.
- To ensure that any divergence among EAM catalog values, the RCM knowledge base, and observed reality are reconciled in a continuous update process.[3]
© 2013 – 2017, Murray Wiseman. All rights reserved.
- [1]Proportional hazard modeling extends the Weibull model by including a second factor
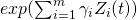 in:
in:
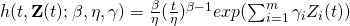
where
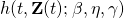 is the failure rate function, β>0 is the shape (age) parameter, η>0 is the scale parameter, and γ =( γ1,γ2,… γm,) is the coefficient vector for the condition monitoring variable (covariate) vector Z(t).
is the failure rate function, β>0 is the shape (age) parameter, η>0 is the scale parameter, and γ =( γ1,γ2,… γm,) is the coefficient vector for the condition monitoring variable (covariate) vector Z(t).The first factor
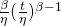 on the right hand side of the equation is recognizable as the Weibull hazard function. ↩
on the right hand side of the equation is recognizable as the Weibull hazard function. ↩ - [2]Catch 22 is the bureaucratic revolving door made famous in Joseph Heller’s 1961 satiric novel of that name. LRCM circumvents “Catch 22” by making it easy for technicians to provide the right failure mode and event type information consistently. Trying to glean predictive content from condition data alone without age data correlation has been a challenge in most cases.↩
- [3]More information on the LRCM methodology may be found in the article Mesh: 12 steps to achieving reliability from data.↩
