The elusive P-F interval

Numerical example

A CBM program on a fleet of Nitrogen compressors monitors the failure mode “second stage piston ring failure”. Real time data from sensors and process computers are collected in a PI historian. Work orders record the as-found state of the rings at maintenance. In the following example, four decisions are generated by the EXAKT software, depending on which of: probability alone, cost, availability, or profitability (cost and availability) has been set as the optimizing objective. The data for this example is available by contacting the author. Background information on this example and the failure mode can be found in (ref. 9).

CBM Report
Decision based on probability
RUL = 106.99616, StdDev = 67.173893

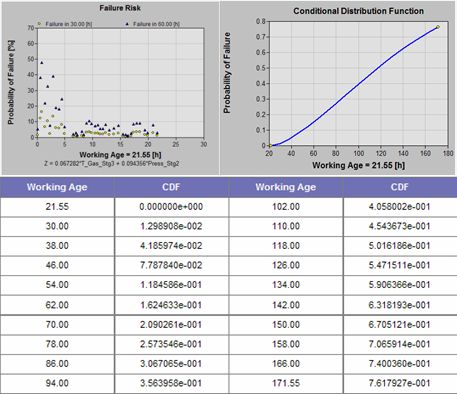
Decisions based on economics and probability
Cost minimization

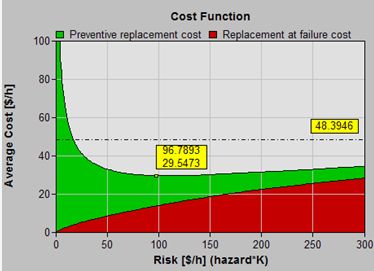	Cost	Prev. Cost	Failure Cost	Preventive %	Expected MTBF (PF or F)
Optimal	29.5473	16.0089 (54.2 % )	13.5384 (45.8 % )	87.6	54.7487
RTF	48.3946	0 (0.0 % )	48.3946 (100 % 0	0.0	123.981
Saving	18.8473 (38.9 % )	-16.0089	34.8562	-83.5	-69.232

Any cost value on the Cost Function graph consists of a red portion, attributable to unplanned failures, and a green portion, representing the average costs associated with preventive maintenance. The green curve determines the optimal risk as its lowest point (96.7893). The table beneath the Cost Function graph summarizes the information. It compares the optimal cost ($30) and optimal mean time between asset renewals (55 h)) of the optimal policy with those ($48 and 124 h) of the “run-to-failure” policy. It quantifies the expected preventive and failure costs ($16 and $14 respectively) and the percentage of incidences (87.6% will be preventive actions while 12.4% will be failures) achieved when adhering to the optimal policy. The table’s content illustrates that the optimal policy will cause us to intervene more often on the average (every 124 versus 55 h), in order to achieve a net per unit saving (of $19 or 39%).

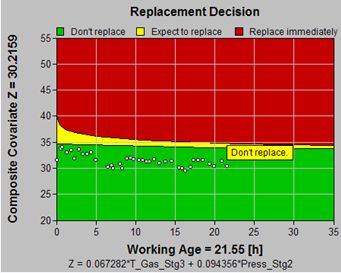Input Parameters
Replacement Policy Type	Basic Cost
Preventive Replacement cost C $	1000
Failure Replacement cost C+K $	6000
Inspection Interval h	30
Decision Parameters
Recommendation	Don’t maintain
Expect to replace in	39.794

Conclusions

The fourth option in the numerical example, optimizing for both low cost and high availability, resolves the difficult problem of deciding upon a CBM (data interpretation) policy or decision model in the light of actual maintenance and business factors. The feature encourages maintenance managers and engineers to elicit good cost and availability information because now they can use it effectively in their decision process. Maintenance and reliability engineers will apply the proposed method based on the EXAKT software to situations where abundant condition monitoring data coincides with the experience of failures and potential failures as recorded in the CMMS.

In this article, we provided an alternative to the difficult, subjective, and often impossible task of choosing a P and P-F interval for use as a CBM decision making procedure. We described a general methodology whereas Reference 1 describes only two special cases (totally random and totally age dependent) for the application of the P-F interval. In the experience of the authors a mix of random and time based behavior characterize the majority of failure modes where CBM will be of use.

Finally, it is necessary to point out that maintenance engineers, frequently, encounter a practical problem when constructing CBM decision models (or when performing any type of reliability analysis). Despite the long time use of elaborate maintenance information relational database systems, reliability analysts find that they lack “age data” required for study and modeling. To resolve this issue, the authors developed a novel process for work order completion that links the work order to the knowledge repository. It has built such a knowledge management system into the new version of the EXAKT product.

Acknowledgement

We are grateful to Dr. Dragan Banjevic of the Center for Maintenance Optimization and Reliability Excellence for his assistance and suggestions.

References

1. John Moubray, RCM II 2nd ed. Butterworth-Heinnemann, 2001 pp 164-5 “How to determine the P-F Interval … A rational approach”.

2. A.K.S. Jardine, D. Banjevic, N. Montgomery, A. Pak., Repairable system reliability: recent developments in CBM optimization, CORS / Optimization Days 2006 Joint Conference, Montreal, May 8-10, 2006

3. Makis V., Jardine A.K.S., Optimal replacement in the proportional hazards model, INFOR, Vol. 30, pp. 172–183, 1991.

4. Aven T., Bergman B., Optimal replacement times – a general set-up, Journal of Applied Probability, Vol. 23, pp. 432–442, 1986.

5. Jardine A.K.S., Banjevic D., Wiseman M., Buck S., Joseph T., Optimizing a mine haul truck wheel motors’ condition monitoring program, JQME, Vol. 7, pp. 286–301, 2001.

6. Lin D., Wiseman M., Banjevic D., Jardine A.K.S., An approach to signal processing and condition-based maintenance for gearboxes subject to tooth failure, Mechanical Systems and Signal Processing, Vol. 18, pp. 993–1007, 2004.

7. Banjevic D., Jardine A.K.S., Makis V., Ennis M., A control-limit policy and software for condition-based maintenance optimization, INFOR, Vol. 39, pp. 32–50, 2001.

8. Banjevic D., Jardine A.K.S., Calculation of reliability function and remaining useful life for a Markov failure time process, IMA Journal of Management Mathematics, [Online] doi:10.1093/imaman/dpi029, 2005.

9. Optimization of Bellis & Morcom 3rd-stage piston ring CBM model, OMDEC case study, Optimization of Bellis & Morcom 3^rd-stage piston ring CBM model, http://www.omdec.com/articles/p_recipN2Compressors.html

© 2011 – 2015, Murray Wiseman. All rights reserved.