The elusive P-F interval

This article discusses the P-F Interval for CBM decision making, its areas of usefulness, and those areas where it is inadequate as a predictive maintenance strategy. An alternative more general approach based on the EXAKT system is proposed. Two categories of decisions, the first driven by failure probability, the second driven by both failure probability and economics are described. Under the second category there are three possible decision strategies: cost minimization, availability maximization, and profitability (considering both cost and availability) maximization. A numerical example illustrates all four types of decisions.

Background

When an item’s functional capacity falls below its required capability we consider the asset to have “failed”. Maintenance restores or preserves an item’s functional capacity to a level exceeding that required by its users. Of the two types of maintenance, reactive or proactive, users specify the latter in certain situations. When the failure would interfere significantly with military readiness or with the goal to produce goods or services, safely, at a profit, and without violating environmental norms, the user will generally request some form of proactive maintenance.

To mitigate the consequences of failure, maintenance managers lean towards a proactive maintenance policy referred to as condition based maintenance or CBM. CBM is also known (with varying nuances) by the names “on-condition maintenance”, “predictive maintenance” (PdM), “condition monitoring” (CM), “prognostics & health management” (PHM)^[1], “equipment health monitoring” (EHM), or simply “preventive maintenance (PM) inspections”.

All of these refer to the gathering, processing, and analyzing of relevant data and observations, in order to make good and timely decisions on whether to:

1. Intervene immediately and conduct maintenance on an equipment at this time, or to
2. Plan to conduct maintenance within a specified time, or to
3. Defer the maintenance decision until the next CBM observation.

When managers and engineers select a task to manage the consequences of a particular failure mode, they tend to consider CBM first. CBM, if applicable, is felt to be more “conservative”, less costly, and less disruptive than TBM (time based maintenance). The graph of Figure 1 represents the well known theory of CBM. It defines CBM as the detection of a potential failure^[2] that the organization has to deal with in a timely manner. P is the initial point at which an evolving failure can, using the current detection technology, be observed. The actual discovery of the potential failure occurs at the subsequent CBM inspection following P.

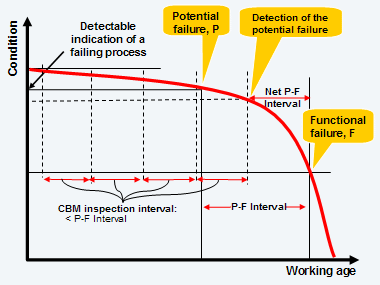
Figure 1 The classical CBM model

Discussion

The graph of the Figure 1 to the left illustrates constraints that the maintenance engineer should account for when designing a CBM program. The Net P-F interval must provide adequate time for the maintenance organization to react from the moment that a potential failure is detected. If it is practical to monitor at the frequency necessary for that to occur, the CBM program is said to be “technically feasible” or “applicable”. In the worst case, according to the graph, if an inspection predates the potential failure by only a small amount, the subsequent inspection will still catch it in time, provided that the maintenance organization is capable of acting within the net P-F interval. If, in the long run, the repetitive proactive task succeeds, at an acceptable cost, in the avoidance or mitigation of the consequences of functional failure, the CBM program is said to be “effective” or “worthwhile”.

The Figure assumes that:

1. the potential failure set point, P, of an identifiable condition of deterioration is known, and that
2. the P-F interval is known and is reasonably consistent (or its range of variation can be estimated), and that
3. it is practical to monitor the item at intervals shorter than the P-F interval

The classical CBM decision model of Figure 1 depends heavily, therefore, on prior knowledge of P and of the P-F interval. In RCM practice, a first approximation of the P-F Interval is gained through consensus by subject matter experts ^[3].

Obstacles to the application of Figure 1

Moubray, in ref. 1, suggests that if P is not known or if P-F cannot be approximated, CBM is not technically feasible. This would rule out a large number of currently active condition monitoring programs. Of the two concepts, “P” and “P-F”, it is the former that poses the greater challenge. Without “P” the P-F interval remains elusive. For this reason, before addressing the P-F interval, we must first discover when and how to declare a potential failure.

In Figure 1, “P” (the point at which currently available technology can detect a failing condition) is flagged at the attainment of a specified value of some condition indicator. Finding an indicator that broadcasts the state of a targeted failure mode is a challenge in itself. In all but the simplest situations, extracting a condition indicator (feature) that faithfully tracks diminishing failure resistance, related to a targeted failure mode (aka cause or mechanism), requires considerable knowledge based on, either:

1. An engineering model of the failure mechanism, or on
2. Prior experience of failure or, preferably, potential failure.

In this discussion we will assume that a physics based model is unavailable. We will focus on the second, arguably, more general case. Once a condition indicator has been proposed that reflects deterioration in a component, we still have to set the decision (potential failure) point P, which, in the absence of a model that describes the physics of the failure mode, requires a methodology of some kind.

This (setting of the declaration level of the potential failure) is the problem encountered by many asset managers deluged with condition monitoring data. Unavoidable questions face any implementer of a CBM program. They are, “Where to set the potential failure?”, and, “Which indicator, from among many monitored variables, should he use for this purpose?” When the physics of the situation are not well known (as is often the case), a “policy” for declaring a potential failure is far from obvious.

Why does Figure 1 and the determination of P and P-F stubbornly elude our grasp? The reasons are:

1. although it does not imply this, one may mistakenly infer from the graph of Figure 1 that, in general, a single condition indicator influences failure probability. Often, however, the problem is multi-dimensional. Where a significant variable is a linear combination of several risk influencing factors, this is a more complex function, which, generally, is not easy to force into the simple P-F model.
2. P and P-F can be random variables. Attempts to set these as fixed decision parameters often lead to frustration.
3. the declaration of P may not be constant for different working ages of the item. A high vibration level in an older item may indicate impending failure while the same vibration level in a younger item may be normal. In general we require some method of determining the three-way (age vs. CBM Indicator vs. reliability) relationship.
4. the P-F example graphs illustrated by Moubray (reproduced below) address actually two extreme cases. In the first case (“Special Case 1” below), known as random behavior, there is no relationship between failure probability and age. (F₁, F₂, F₃ occurred at random ages.) In the second (“Special Case 2”), failure depends entirely on age. The following three paragraphs discuss the confusions that can arise from generalizing from these special cases.
   1. Ref. 1 correctly describes the first case as a situation where conditional failure probability depends entirely on a condition indicator and is
      

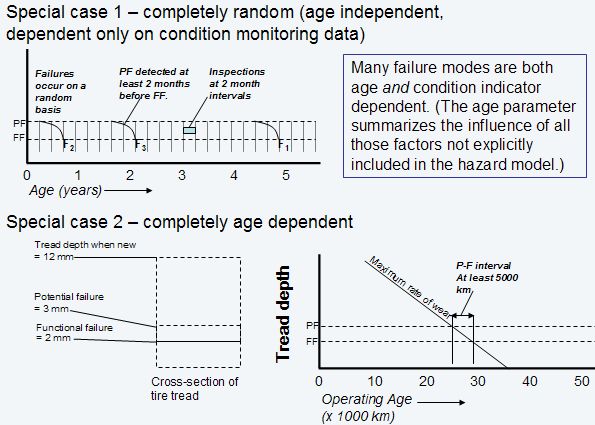
      CBM special cases

      completely independent of age.

   2. A confusion arises in the second case, where ref. 1 also indicates that failure depends on the condition indicator. Ref. 1 fails to mention, however, that the condition indicator (in this case, the tread depth on a tire) is a variable that is equivalent to the component’s age. Such an indicator is, in this simplistic case, a direct measure of accumulated external stress, which is the “working age”. In fact, failure is often defined directly in terms of that measure. For example when the tread depth of an airplane tire reaches a specified minimum, it is considered to have failed because it can no longer preserve the function of the carcass “to be retreadable”. In complex (general) situations, the condition indicator or monitored variable, usually, is not equivalent to working age. Neither is it, generally speaking, so obviously related to potential failure. Implementers of CBM face the challenge of discovery of the precise relationship between relevant condition monitoring data and survival probability.
   3. In practice, failure often depends both on age and on one or more condition indicators. (We might consider the age dependence as an averaging of a multitude of other undetermined factors.) For this general case more advanced methodologies are required with which to reveal the potential failure and to determine the P-F interval.

Making CBM decisions in EXAKT

EXAKT handles the multi-dimensionality of CBM, the probabilistic nature of failure, and the influence of working age, by providing two ways of deciding whether an item, component, or failure mode is in a potential failure state. Furthermore, if the item is not currently in a “P” state, EXAKT still provides an estimated time to failure or a remaining useful life estimate (RULE). The two decision processes can be categorized as:

1. a decision based on the combination of failure probability and the quantifiable consequences of the failure, and
2. a decision based solely on failure probability.

The first CBM decision making strategy will support decisions related to operational and non-operational consequences of failure whose economic impact can be estimated, for example, the failure of a component in a production line. The second method will apply to decisions that must be based strictly on probability. These include situations beyond the expected, whose failure costs are unknown or incalculable, such as where catastrophic environmental, health, and safety consequences are concerned. Managers use both types of decision methods regularly within the scope of their responsibilities. The flow diagram of Figure 2 summarizes EXAKT’s functionality in both these decision processes.

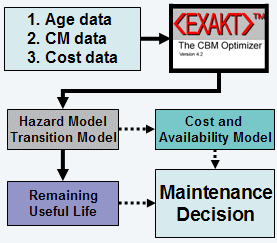
Figure 2 Two decision paths

Figure 2: Flow diagram of EXAKT. Age data is also known as “life” data, and consists of the working age and type of event (failure or suspension^[4]) defining each life ending. CM data is “condition monitoring” data. “Cost data” defines the ‘penalty’ or average costs associated with failure compared to the average cost of preventing the failure.

Most decisions in maintenance are driven not only by considerations of asset survival probability but also by economic factors.

Where business dynamics are concerned, managers quickly appreciate the need to optimize decisions in the face of competing objectives. A policy is a procedure (model) for making the best decisions given the evidence of the moment. Achieving value from our decision policy depends on:

1. Having the right data, and
2. Transforming that data into the correct (best) course of action

The maintenance engineer and his manager must, therefore, understand and agree upon the meaning of “best” in the current operating context. Defining “reliability” in the general sense of the word (not the mathematical sense), we may say that it is: The achievement of a desired production rate, quality, availability, mission survivability, at lowest cost, safely, and without infringing environmental norms.

The seven desirables: 1. production rate, 2. quality, 3. availability, 4. mission survivability, 5. lowest cost, 6. safety, 7. environmental integrity are rarely mutually inclusive. They usually conflict. If you turn up the speed knob on the production rate, this may adversely affect quality (ultimate yield). If you run your equipment to failure, it may give an acceptable availability, but could increase costs. And so on, and so forth.

The possibilities among these objectives are endless. Given this vastness of variety of outcomes of a decision process, it is no wonder that maintenance departments struggle to pinpoint the elusive “reliability” bull’s eye. When faced with conflicting objectives, managers recognize the need to strike a compromise.

Compromise in maintenance leads one squarely to the topic of optimization. The EXAKT optimization process helps reduce a diversity of objectives to a common denominator, so that the decision process issues the best trade-off among several goals. In the numerical example to follow we show the way in which EXAKT balances the aims of low cost and high availability in an optimized CBM policy. But first let us discuss the subject of optimization with respect to the objective of cost.

In general, neither P nor F happen at fixed times nor under fixed conditions. Rather, they occur randomly according to probability distributions. EXAKT is a probabilistic approach that decides, based on current condition relative to an optimal hazard level, whether maintenance is needed. The difference of approaches will be explored in this article. In maintenance, the uncertainty of the time of failure is the reality. The increasing temperature of a bearing, a differential pressure increasing linearly across a filter, or the treads of an airplane tire wearing down in proportion to the number of landings, are all special deterministic cases of CBM, characterized by fixed P and F states. The development of cracks in a mechanical component is more stochastic. Maintainers must adopt tools and procedures that deal with the general, probabilistic, and more frequent cases. The more general, the more accurate.

We intend to show (on pages 2, 3, and 4) how the problem can be addressed clearly only when approached in a statistical way. We will talk about managing uncertainty in order to make a strong case for how the simplified or approximate (P-F interval) approach will not lead, generally, to results that deal realistically with changes in the resistance to failure.

© 2011 – 2015, Murray Wiseman. All rights reserved.

1. ^[1]Not to be confused with “Proportional Hazard Model” aka PHM used in EXAKT↩
2. ^[2]A potential failure is a developing failure whose direst consequences are imminent. Should nothing be done to mitigate the impending loss of function, the failure will usually result in serious consequences to the organization.↩
3. ^[3]Reference 1: John Moubray, RCM II 2nd ed. Butterworth-Heinnemann, 2001 pp 164-5 “How to determine the P-F Interval … A rational approach”↩
4. ^[4]A suspension is a renewal of a part or failure mode for reasons other than failure.↩