P-F Interval a red herring?

The article describing EXAKT CBM optimization, “The Elusive P-F Interval“, may leave one with the impression that the P-F Interval is an irrelevant concept. The P-F Interval is a useful concept in certain simple cases. Nevertheless, it does detract from an issue of greater concern to the designer of a CBM program. Namely, the reliable detection of  the potential failure “P”.

NAVAIR 00-25-403^[1] calculates the CBM inspection Interval as  I= PF/n where n would depend on:

1. Probability, θ, of detecting a potential failure with one occurrence of the proposed CBM task, assuming the potential failure has occurred, and
2. Acceptable probability of failure (P_acc).

Although much focus is placed by RCM practitioners on the PF Interval, neither Nowlan and Heap, nor Moubray intended that it be used for more than a rough first approximation of a CBM inspection interval. The interval for inspection would subsequently be refined in the context of a continuous improvement process.

Once a model or rule for declaring potential failure has been adopted, confirming evidence from work orders in a LRCM program (see the five steps below) will provide more information on the actual rate of degradation in order not only to sharpen the inspection interval but, more importantly, to achieve confidence in the declaration of P itself.

The following graph explains “Classical” CBM theory:

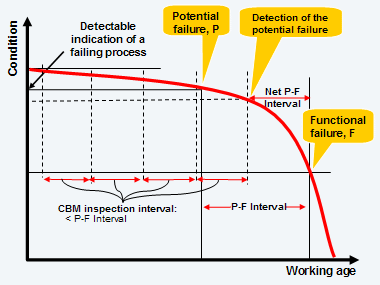
Maintenance “Lead Time” is the time required for maintenance to respond to a P alert. In the worst case, according to the graph, if an inspection predates the potential failure by only a small amount, the subsequent inspection will still catch it in time, provided that the maintenance organization is capable of acting within the Net P-F interval.

From the graph, the Net P-F will always be greater than PF/2 (when I = PF/2). If n =3 then the Net P-F will be greater than 2PF/3, and so on. Thus we must choose an “n” such that the Net P-F is greater than the Lead Time. The bigger the value of n used, the smaller the inspection interval, and the more costly (presumably) will be the CBM policy.

The P-F interval, while a simple model to explain CBM, is a difficult procedure. Discovery of the P-F interval requires repeated experience of having detected and reacted to P. On the other hand, in order to have a rule with which to declare P we need the experience of having applied the P-F model. The EXAKT/LRCM process gets around this circularity with a Remaining Useful Life (RUL) model that derives from CBM data and related work order data representing instances of failure modes. The model, when applied day-to-day, not only provides practical CBM decisions but also tracks and improves predictive confidence. Additionally, the model supports the continuous improvement of CBM inspection intervals by reporting confidence intervals of Remaining Useful Life Estimates (RULEs).

Summarizing, reliability engineers should concentrate their efforts in finding a reliable, unambiguous, and confirmed method for declaring “P”. They can accomplish this using EXAKT and LRCM whereby failures are differentiated from suspensions on work orders. The following steps describe the LRCM process:

1. On the work order discriminate between failures, confirmed potential failures, and suspensions when closing work orders.
2. Continuously improve the RCM knowledge base when closing work orders  by using the LRCM knowledge feedback function.
3. Link work orders to RCM knowledge records by using the LRCM user interface to complete the work order.
4. Synchronize EAM failure codes and catalogs with the RCM knowledge base using the LRCM synchronization function.
5. Perform CBM analysis and optimization using EXAKT.

© 2011 – 2015, Murray Wiseman. All rights reserved.

1. ^[1]Guidelines for the naval aviation Reliability-centered maintenance Process, 2 July 2005↩