In the context of maintenance and reliability, “simulation” refers to Monte Carlo Simulation (MCS). MCS generates and uses a stream of random numbers to represent failure (cumulative) probabilities and repair duration (cumulative) probabilities. It substitutes these random numbers for F(t) in the cumulative failure probability equation (for example equation 1 below) and solves for t. It repeats the calculation for each of the components in the system, thereby generating lists of their failure times. MCS uses the same technique to generate a list of component repair times (duration of each repair) corresponding to the stream of random number probabilities.
Examples of a failure and repair duration distribution are respectively:
Cumulative Failure Distribution: ![]() (eqn. 1)
(eqn. 1)
Cumulative Distribution of Repair Durations: ![]() (eqn. 2)
(eqn. 2)
Assume, for a component whose failure and repair time distributions are those of Equations 1 and 2 respectively, and that the first random number generated for failure probability F(t) is 0.647552.[1] Solving for t yields t = 1621.118 days. Similarly if the first randomly generated number representing the cumulative probability for a repair duration[2] F(t) is 0.034957 the software can find the repair duration t = 2.645032 days.[3] The software registers the fact that this component will be unavailable during the time from 1621.118 days to 1621.118 + 2.645032 days?” The calculations are repeated for each probability value in the two respective random number streams yielding a set of failure times and repair durations for the given component.
This component is one of many components with differing failure and repair distributions, each with its own set of failure times and repair durations. The components operate in a system design configuration of series and parallel paths.
A “trial” consists of the following steps: The algorithm, at time t asks, “Is the system operational?” The answer is negative if there is a failed component whose backup component(s) is also in a failed state? The algorithm executes the next trial by incrementing the time to t=t+Δt and asking the same question again. If in a trial, the system is out of operation the algorithm registers that fact and accumulates the downtime until a subsequent trial determines that the system is back up.
Trials are performed until t exceeds the stated time for a single virtual mission (called a “run”). The simulation is performed over many runs (a thousand or more). By averaging the numbers of system failure events and their durations MCS forecasts the reliability, availability, and maintenance cost of a given design, usage profile, and maintenance policy. The combination of a proposed design, usage pattern, and maintenance strategy can be thought of as a “scenario”. By comparing the costs and reliability performances of a variety of simulated scenarios, the analyst can propose optimal ones and can predict their respective performances in terms of:
- Mean Time Between Failure (MTBF) of the system;
- Availability;
- Expected costs;
- Expected down time;
- Expected spare parts usage;
- etc.
Simulation is used in the system design phase in order to select components and their configurations from several alternatives. The combination that meets the requirements or provides the best compromise between cost, reliability, and system performance is then retained for production. Design software incorporating MCS provides a number of standards libraries containing the failure distributions of a large number of commonly use electrical and mechanical parts. Once the equipment is built and put into service, simulation can be a useful tool in the operational phase as well, provided that LRCM procedures are in place to obtain accurate failure, suspension, and repair times. Clockwork Solutions Inc. has combined Monte Carlo simulation[4] with EXAKT CBM Proportional Hazard Modeling to refine prediction performance with the benefit of sensor and condition monitoring data.
© 2011 – 2014, Murray Wiseman. All rights reserved.
- [1]Since these are cumulative probability distributions their values will range from 0 to 1.↩
- [2]which would include all the downtime to diagnose, gather parts and personnel, and test the system before returning it to service.↩
- [3]The repair duration is obtained from the inverse standard normal CDF:
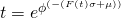 ↩
↩ - [4]in its SPAR PHM product↩
