Abstract – Does condition monitoring deliver the results you expect. Can we sharpen the saw and make a more informed reliability decision? The project investigated the use of a Maintenance Decision Support tool and how it may be used to improve reliability decisions based upon failure prediction. Data collection and manipulation proved to be the single most challenging issue. The accuracy with which failures are reported in the Computerised Maintenance Management System (CMMS) and the need to understand which failure modes actually occurred and whether they really failed or were suspended was shown to be of prime importance if reliability analysis was to succeed. The effort needed by the Reliability Engineer in performing reliability analysis pales in comparison to that required for the cleansing of the data and for its transformation into analyzable form. Once good data emerges from the anarchy of styles used within the CMMS, software makes light of the task of detailed reliability analysis that will enable good maintenance decisions.
I INTRODUCTION
This paper provides an insight into the challenges faced by the Reliability Engineer before he can exploit Maintenance Decision Support software. The intent of this study is to apply such a tool [1] to critical magnetic pumps at the Orica Laverton North Chloralkali Plant in Australia. Conditioning Monitoring (CM) already existed. Nevertheless unexpected failures have occurred and the need to validate and improve on the CM process was paramount. Reliability based decisions may be assisted with specific types of data relating to equipment operation and maintenance. However, it is important to recognize that large volumes of CM data are no guarantee of good condition based maintenance decision models unless that data reflects the deterioration of failure modes that actually occur. How do we know what condition monitoring variables are significant? This project will attempt to use a software tool that analyses CMMS failure data in conjunction with condition monitoring data in order to identify those monitored variables that influence the probability of occurrence of the targeted failure modes. The methodology applies a Proportional Hazard Model (PHM) [2]to determine not only which monitored variables are significant but also the precise probabilistic relationship between those variables and equipment failure. The main objective of this study is to understand the nature of the data required for this. The paper will discuss a data acquisition, cleansing and transformation philosophy for condition monitoring programs that supports practical decision making in maintenance.
II SCOPE
The study was limited to four pump sets over two years, an admittedly small sample. These pumps are all magnetic pumps with induction motors on caustic service as detailed in Table 1 below.
| Tag | Pump Description | Pump Model |
| P12111A | Catholyte Pump A | Magnetic Drive Size 80 |
| P12111B | Catholyte Pump A | Magnetic Drive Size 80 |
| P13005 | Caustic Evaporator Feed Pump | Magnetic Drive Size 40 |
| P13006 | Intermediate Caustic Pump | Magnetic Drive Size 40 |
| P12111AM | Catholyte Pump A Motor | Induction Motor 11kW |
| P12111BM | Catholyte Pump B Motor | Induction Motor 11kW |
| P13005M | Caustic Evaporator Feed Pump Motor | Induction Motor 15kW |
| P13006M | Intermediate Caustic Pump Motor | Induction Motor 15kW |
III RELIABILITY PREDICTION MODELS
There are many reliability prediction software tools on the market. A basic search on the web reveals a number of vendors [1], [2], [3] for example. This project aims to try out one such program, EXAKT© because it is one of the few that confronts the challenge of achieving verifiable day-to-day decisions based upon the two principal available maintenance data sources: the CBM database(s) and the CMMS database.
Reliability prediction is not new. One of the most widely recognised models was developed by Weibull in 1951 [4]. He developed a failure analysis method that provided reliability predictions as well as the level of confidence with which those predictions may be applied.
Weibull Distribution – three of its forms
Cumulative distribution ![]()
Hazard ![]()
Probability density ![]()
Where:
β (beta) is the “shape” parameter,
η (eta) is the “scale” parameter, and
t is the working age of the item or failure mode being modeled.
Weibull also showed that the shape parameter β in his equation (above) relating reliability to age provides an indication of likely failure behavior. For a shape parameter of β <1, the Weibull model predicts infant mortality due to poor material quality, incorrect installation, or faulty start up procedures. If b =1 the failure behavior is random, meaning that the failure rate (or conditional probability of failure) is constant and does not change with age or usage. Finally, for β >1, the Weibull model predicts that the failure rate will increase with age due to wear out. Based on the Weibull model having determined that β =< 1 it may be concluded that age based replacement programs, rather than improve performance, could, on the contrary, lead to unnecessary costs, downtime, and poor reliability. If a maintenance strategy called for a randomly failing component (with β = 1) to be replaced preventively at an interval equal to its MTBF = η, then 63% of the time that component would fail prior to PM.
To develop a Weibull model we need only determine (estimate from historical data) values for the parameters β and η. The model will yield a variety of data points revealing of the relationship between age and reliability. These relationships when represented graphically help us understand the age based failure behaviour of items and, more usefully, their failure modes.
The problem with age based analysis
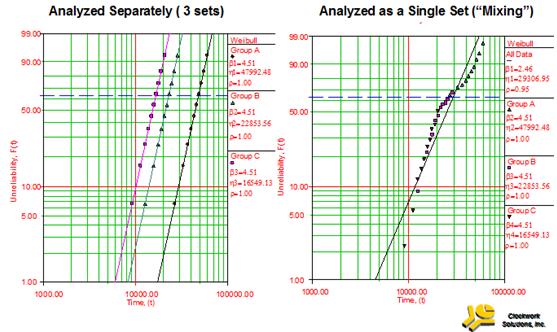
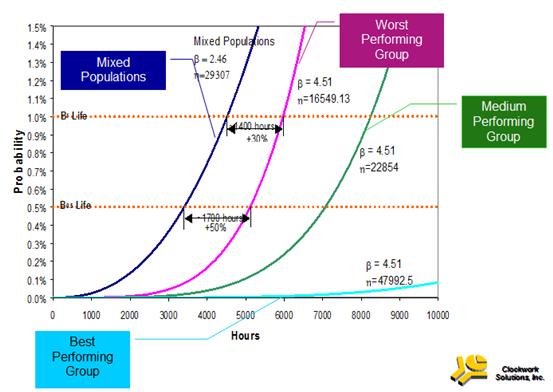
With basic Weibull (age based) analysis practical decision making will often be problematic if populations are mixed or varying conditions influence individual units in the sample. In those cases basic Weibull analysis will tend to underestimate the shape parameter b leading to underestimation of the equipment life. Figure 1 and Figure 2 illustrate a general problem when maintenance engineers use an age-based analysis for proactive decision making. The analysis can often lead to higher than necessary preventive replacement frequencies and costs.
Apart from the problem of mixed populations, making individual unit repair-now or continue-to-operate decisions armed only with an item’s age is of little value in day-to-day operations. Age in the age-reliability plot is, in essence, a mixture that averages out the effects of other influential yet unspecified variables. Age alone, therefore, obscures the influence of a unit’s individual operating conditions and its current state as reflected by its condition monitored data. This reality has lead to a maintenance strategic approach known as Condition Based Maintenance (CBM).
How can Weibull analysis be extended to cover CBM?
Proportional Hazard Modelling (PHM) extends the Weibull method to cover today’s CBM reality. It resolves the problem of mixed populations by including, not only age, but also other significant differentiating factors (operational and monitored) in the analysis. The procedure makes use of today’s inexpensive personal computers to handle the intensive computational requirements
PHM attempts to “sharpen the saw” by using all available significant prediction factors. These include other plant data obtained from condition monitoring and operational records. The modelling process tests for failure predictability from each available data source. It attempts to identify the significant variables that influence the probability of occurrence of the failure modes of interest.
The outcomes from this approach would typically reduce the Weibull shape parameter b such that age based decisions will be superseded gradually (as information management procedures improve) by condition based decisions. Such an evolution in maintenance practice is desirable because condition based decisions tend to be more[3] conservative and less costly in the long run than age based decisions. This is due primarily to the fact that CBM tasks (when executed using a decision model based on significant variables) detect potential failures whereas age based preventive maintenance tasks, even if performed excessively frequently, do not totally exclude the possibility that some items will fail functionally. The consequences are higher costs. Confidence in CBM prediction is a function of how correlated the condition monitoring variables are to the failure modes’ deteriorations. The existence of such correlations can be more reliably determined when failures and suspensions[4] are accurately distinguished from one another in the CMMS.
Business factors, when combined with the proportional hazard model, yield an optimal decision chart (Figure 3A). The chart plots the progressive likelihood of failure and of risk. “Risk” combines both probability and cost. A “crossover” point suggests the optimal moment for repair. The user may set his optimizing objectives in the model. For example, the objective (of a given CBM task relevant to a given failure mode) may be set for cost, availability, profitability or a desired mix of all three. The method also provides a remaining useful life (RUL) estimate and confidence interval (Figure 3B) independently of economic factors.
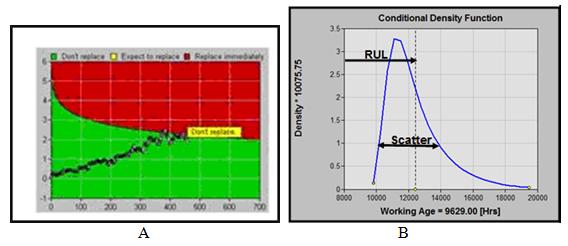
- Figure 3A Optimal decision chart. Vertical axis: the weighted sum of the values of each CBM variable determined to be significant in the model. Horizontal axis: the current age of the item. Green area: No action. Yellow area (small area between the green and red boundaries): Action required in a specified time. Red area: Action recommended as soon as possible (Item is in a “Potential Failure” state). Figure 3B Conditional Probability Density provides estimation of Remaining Useful Life (RUL) and confidence (standard deviation) based solely on probability.
A decision model, such as that illustrated in Figure 3, which is based both on cost and probability will identify the most cost effective moment of intervention (given the current working age and the most recent levels of the significant monitored variables).
The two most important organizational requirements for CBM modelling (or for any form of data based reliability analysis for that matter) are that:
- The failure modes be well identified on the completed work orders, and that
- The distinction be made between failure (or impending failure) and preventive replacement (suspension of a component’s life cycle).
In a “proportional hazard model (PHM) analysis, the equation of Figure 4 is numerically solved.
As an example the right hand side of the PHM equation in Figure 4 might be ![]() where (in this example) the shape parameter ß is 0.781 and the scale parameter η is 2709 and there are two significant CBM variables, MaxWSDrop and AccFreezRain, whose parameters γ1 and γ2 are 0.06944 and 2.49 respectively.
where (in this example) the shape parameter ß is 0.781 and the scale parameter η is 2709 and there are two significant CBM variables, MaxWSDrop and AccFreezRain, whose parameters γ1 and γ2 are 0.06944 and 2.49 respectively.
The PHM software applies statistical tests for the model fit and for the significance of variables associated with the failure modes and for the overall models goodness of fit.
© 2011, Ron Jenkins. All rights reserved.
- [1]EXAKT© CBM Decision Optimization (www.omdec.com/wiki)↩
- [2]See Reference 8.↩
- [3]“More conservative” in the sense that because CBM (assuming that the CBM detection confidence is high enough) detects “potential” failures, which, by definition, have few or minor consequences. Hence fewer functional failures, having severe consequences, will slip through.↩
- [4]A suspension is a renewal of a part or component (failure mode) for any reason other than failure. Without making the distinction between failure and suspension on the completed work order, no data based reliability analysis will be possible.↩