Conditional failure probability, reliability, and failure rate

What is the relationship between the conditional failure probability H(t), the reliability R(t), the density function f(t), and the failure rate h(t)?

In the article  Conditional probability of failure we showed that the conditional failure probability H(t) is:

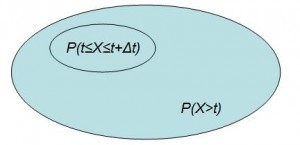
X is the failure time. By definition the denominator is the survival or reliability function at time t, i.e. P(X>t) = R(t). The Conditional Probability of Failure is a special case of conditional probability wherein the numerator is the intersection of two event probabilities, the first being entirely contained within the probability space of the second, as depicted in the Venne graph:

Therefore the numerator, which is the intersection of P(t≤X≤t+Δt) and  P(X>t) reduces to simply  P(t≤X≤t+Δt). Also, by expressing P(t≤X≤t+Δt) as the difference between the Cumulative Failure Probabilities calculated at t and t+Δt  the numerator can be expressed as the change in Reliability over the interval Δt as:

P(t≤X≤t+Δt) = F(t+Δt) – F(t) = 1-R(t+Δt) – (1-R(t)) = R(t)-R(t+Δt)

where the Cumulative Failure Probability F(t) and the Reliability R(t)  are complements, i.e. F(t) = 1-R(t), so that

We define the failure rate^[1] h(t) as the limit of the ratio H(t)/Δt as Δt→0:

Differentiating we have the density function f(t):

:

Then

© 2014, Murray Wiseman. All rights reserved.

1. ^[1] also called hazard function or hazard rate↩