Availability as the optimization criterion
The Reliability Engineer can use EXAKT to develop a maximum availability model. In order to do so, the analyst must supply the parameters for this strategy. These are fixed values for the downtimes incurred by:
- Preventive renewal (maintenance), and
- Renewal as a result of failure.
The costs of materials and labor are not considered significant in this option, or they are believed to be proportional to downtimes and, thus, can be ignored. The optimal strategy maximizes expected availability per unit time. Availablity is defined as
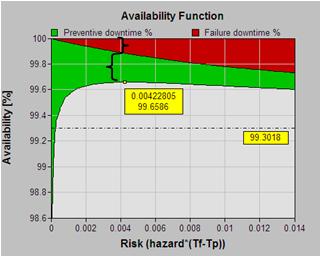
The software finds the CBM and age control limits that, if acted upon consistently by the maintenance department, will result in highest availaiblity. The optimal decision model is found by maximizing the availability function:
Figure 5 Availability optimization input form
Where:
AE is the total expected Availaiblity per unit of working age or production of the asset (Item, Failure Mode)
Q is the failure probability
W is the expected working age at failure
Tp is the downtime required by preventive maintenance.
Tf is the downtime resulting from a failure.
Figure 6 Availability function graph
The example illustrates the trade-off made in optimizing for availability. In the preceding cost model we “bought” lower overall cost by “paying” for it with more frequent intervention.
We assumed that the time-to-repair was negligeable, or was proportional to the cost, and therefore could be ignored. The difference between failure and preventive repair costs dictated the exact nature of the compromise in order that overall impact on the per unit production cost be minimum.
| Table 2 |
|---|
 |
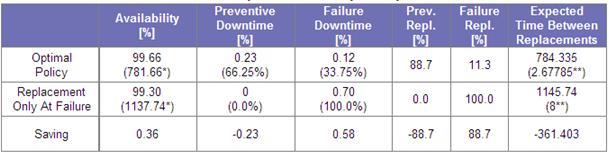In a symmetrical way, the maximium availability model focuses completely on downtime. In this example, we have “bought” high availability by paying for it with more frequent intervention. We assumed that the cost of repair was negligeable, or was proportional to the repair time and therefore could be ignored. The difference between failure and preventive repair times (rather than costs) dictated the exact nature of the compromise to achieve high equipment availability.
© 2011 – 2015, Murray Wiseman. All rights reserved.
- Optimizing a Condition Based Maintenance Program with Gearbox Tooth Failure (100%)
- EXAKT cost sensitivity analysis (100%)
- Thoughts from a mine maintenance engineer (100%)
- RCM - Reliability analysis in more than two dimensions is CBM (76.4%)
- Warranty for haul trucks (56%)
- Predictive analytics (RANDOM - 44%)
[…] that will enable the maintenance engineer to arrive at a general policy. The article “CBM Optimization” describes the analysis […]
[…] The entire exercise above, onerous as it appears, can be executed in less than ten minutes, once you gain some familiarity with the user interface. The mechanics of using the EXAKT program are, in actuality, the easiest part of the CBM decision modeling process. The more difficult part of the process begins with the maintenance work order. Specifically, the work order form wherein the technician enters the right data. The true challenge lies in understanding the nature of data. The type and quality of data required for the above analysis is explained in the article CBM Optimization. […]
[…] such as EXAKT, see https://www.livingreliability.com/en/posts/cbm-optimization/ […]