What is the scale parameter?

In Weibull analysis, what exactly is the scale parameter, η (Eta)? And why, at t = η , will 63.21% of the population have failed, regardless of the value of the shape parameter, β (Beta)?

η (Eta) is called the “scale parameter” in the Weibull age reliability relationship because it scales the value of age t. That is it stretches or contracts the failure distribution along the age axis. This is why it is called “scale parameter”. Its value and unit are determined by the unit of age, t, (e.g. hours, fuel consumed, rounds fired, etc.).

Consider the Weibull equation for the Cumulative Distribution Function letting t = η (Eta).

(1)  

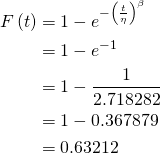
For random failure η is the MTTF. However, it is safe to say that most failure modes ^[1] will fail with a probability > 50% prior to their MTTF.

© 2011 – 2016, Murray Wiseman. All rights reserved.

1. ^[1]Not only those that fail randomly but all that adhere to Weibull behavior (estimated at 80+%). See Failure probability prior to attaining MTTF↩